Modeling Biological Networks
IV.1 Coordinators
IV.2 Participants
IV.3 Introduction
IV.4 Background and Significance
IV.5 Research Plan
IV.6 Specific Subprojects
- IV.6.i Subproject 1 Topological Analysis of Selected Metabolic and Regulatory Networks for Large-scale Structure
- [ Other Subprojects ]
IV.8 Timeline
< Previous | Page 11 of 35 | Next >
IV.6.i.d.1 Clustering algorithms:
Various data-mining applications have motivated extensive investigation of clustering in both applied mathematical and physical contexts. The principle of energy or distance minimization has led to a series of efficient algorithms. Many of these tools use statistical mechanics techniques, such as Ising or Potts (See the discussion in Section VI.7.i.b) models (Bengtsson and Poivainen, 1995) that, under thermal annealing, can explore a significant fraction of the thermodynamically available phase space, effectively optimizing the outcome. In addition, several new clustering algorithms address large networks, such as the WWW or other network-based information architectures. Our goal is to identify from the network topology the existence of underlying communities. As the WWW is a directed network with an underlying scale-free topology, the clustering in computer science resembles that in biochemical networks: finding the natural modules in a directed graph. We plan to implement multiple algorithms to search for modularity first in metabolic networks of E. coli and other bacteria and later in eukaryotes. The simultaneous use of several algorithms and clustering criteria provides confidence in identifying modules.
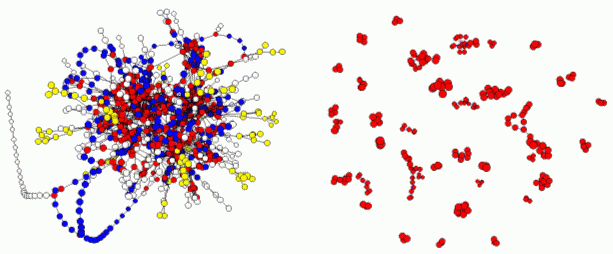
Fig. IV.6. Identifying potential modules through clustering. On the left we show the topology of the E. coli metabolic network, each node corresponding to a metabolic substrate and each link to a reaction. We removed superfluous substrates, like ATP and H2O, from reactions in which they only acted as donor or acceptor molecules, respectively. The colors code topologically distinct pathways. On the right, we show the clusters identified by our clustering algorithm. The figure shows aggregated data, and each tiny cluster can contain anywhere from ten to a hundred substrates (not shown).
IV.6.i.d.1.i Spatial clustering algorithms:
The most popular clustering methods employ "spatial" clustering (Bengtsson and Poivainen, 1995; Jain et al., 2000; Ramal et al., 1986; Chazelle, 2000; Pettie and Ramachandran, 2000; Garay et al., 1998; Rose et al., Fox, 1990a, 1990b, 1993; Jain and Dubes, 1988; Blatt et al., 1996). The number of characteristics assigned to each element determines the dimension of the phase space. The "distance" in this multidimensional space typically characterizes the similarity between a pair of elements with respect to the quantities driving clustering. Each element corresponds to a point in this phase space. Various methods aim to group nearby elements. A common approach builds a minimum spanning tree, whose end nodes are the elements, such that elements close in the phase space root in the same upper level nodes (Chazelle, 2000; Pettie and Ramachandran, 2000; Garay et al., 1998; Ramal et al., 1986).