Cytoskeleton and Cell Motility

V.6.i.b Preliminary Results:

In other work ongoing in the Goodson laboratory, we are determining the affinities of CLIP-170 and CLIP-170 fragments for different conformational states of tubulin/microtubules using established biophysical approaches including sedimentation assays, fluorescence anisotropy, and surface plasmon resonance (BIACore). These affinity determinations, together with previously established tubulin assembly rate constants (Gliksman et al., 1993; Grego et al., 2001; Tran et al., 1997) will provide the necessary binding constants for our quantitative models. Our results indicate that CLIP-170 has high affinity for both polymerized and unpolymerized tubulin (Folker and Goodson in preparation). This first quantitative characterization of interactions between CLIP-170 and tubulin, has interesting implications for the mechanism by which CLIP-170 localizes to microtubule plus ends. Our models also require quantitative information on the effect of CLIP-170 on microtubule dynamics. We are currently determining these parameters with in vitro dynamic instability assays using video microscopy. Preliminary results show that CLIP-170 reduces both the rate and extent of catastrophes. the Walczak laboratory, we are using biochemistry to explore how XKCM1 induces microtubule depolymerization. Our previous work (Desai et al., 1999) showed that XKCM1 binds to microtubule ends, causing a conformational change in the microtubule which promotes depolymerization (Figure V.4). We are taking advantage of our ability to generate various microtubule substrates with different geometries to determine what features XKCM1 recognizes. We have also determined affinity constants for XKCM1 binding to microtubules and tubulin. Preliminary estimates suggest that XKCM1 binds to microtubule ends with an affinity of approximately 10 nM. Together these experiments will provide important information about how XKCM1 specifically targets the end of microtubules so that it can act there. These experimentally derived values will provide the necessary constants for quantitative models as described for CLIP-170 above.

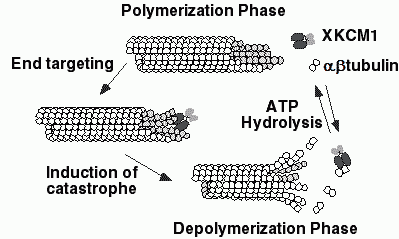Fig. V.4. A model for how XKCM1 may destabilize microtubules. XKCM1 targets the end of the MT, where binding induces a conformational change in the MT lattice. This conformational change disrupts the lattice and induces MT depolymerization which releases tubulin dimer as well as tubulin dimer associated with XKCM1. Hydrolysis of ATP couples to the dissociation of the XKCM1·tubulin dimer complex to allow XKCM1 to be catalytic and function on a new MT end.

V.6.1.c Modeling Microtubule Dynamics:

Techniques to describe the dynamic behavior of single microtubules include Monte Carlo simulations, stochastic processes, chemical kinetics equations, and diffusion models (see for example Chen and Hill, 1985; Davis et al., 2002; Flyvbjerg et al., 1996; Grego et al., 2001; Martin et al., 1999 Odde et al.,1995; Hill, 1987). Betts produced a particularly elegant classical, simplified molecular dynamics model which could also simulate large arrays of tubules and their interactions (Betts, 2000). We propose to use two different approaches to model the effects that individual proteins have on the dynamics of microtubules on different scales, keeping in mind that an eventual goal of our modeling is to study self-organization in the microtubule cytoskeleton. First, we intend to use partial differential equation models to describe the effects of CLIP-170 and/or XKCM1 on microtubule dynamics. These simulations will employ the biochemical parameters (affinity constants, effects on dynamic instability parameters) described above. In particular, we will start by analyzing at the scale of protein-tubulin interactions and protein-microtubule interactions and compare to the larger scale model of Flyvbjerg et al. (Flyvbjerg et al., 1996), which extends the classical Oosawa and Asakura approach (Oosawa and Asakura, 1975). For details about different diffusion approximation models of the stochastic microtubule assembly (see, e.g. Maly, 2002). By adding more intermediate stages of assembly to this model and by introducing the interactions and effects of microtubule associated proteins, we will obtain a system of nonlinear equations. We will study solutions of these systems by analytically and numerically simulating the impact of microtubule binding proteins on dynamical instability and, in particular, on the catastrophe rate (e.g. microtubule growth, GTP hydrolysis at the GTP/GDP interface, spontaneous generation of new interfaces ). We will also extend the model by incorporating rescue events.

A second approach will use cellular automata to model microtubule-motor interaction on the microscopic level. Cellular automaton models have successfully modeled motors and interactions between microtubules and free tubulin (Ponce-Dawson et al., 1998). This approach abstracts elements of the microscopic structure of microtubules, such as the lattice of individual tubulin dimers. It allows testing a large range of biological parameters and incorporating new biologically determined parameters. We will eventually extend our cellular automaton models to lattice-Boltzmann models.