Cytoskeleton and Cell Motility

• V.6.v Subproject 5 - Computational Modeling of the Actin Cytoskeleton
  • V.6.v.a Hybrid Stochastic/Reaction-Diffusion Model
  • V.6.v.b Minimum Model of the Globally Interconnected Cytoskeleton

< Previous | Page 20 of 23 | Next >

Section V.6.iv.f.1 discussed a model aimed at understanding of the mechanical properties of cross-linked actin networks. The cytoskeleton and particularly the actin network participates in other vital cell functions like signal and mechano transduction across the cell. Transmembrane adhesion molecules, like cadherins and integrins attach to the actin cytoskeleton and initiate information transfer chains (Juliano and Huskill, 1993; Gumbiner, 2000). Modeling such phenomena requires representing the cytoskeleton over the entire cell. A complete model that used all the biochemical and biomechanical information discussed earlier in this Project would be a hopeless task.

We propose to construct a simplified model cytoskeleton primarily to study phenomena that occur on the cellular scale, like signal and mechano transduction. The particular question to be studied determines the complexity of the model. A full understanding of cytoskeletal organization and function requires detailed biochemical and biophysical information. Elucidating how this interconnected mesh participates in signaling may not. We thus start with a "minimal model" of the cytoskeleton, which consists only of actin fibers and microtubules. We will gradually refine this model using information from other Subprojects. The model relies on published constants (Dufort and Lumsden) and results by Consortium members (Shafrir et al., 2000; Shafrir and Forgacs, 2001).

A typical eukaryotic cell has 2-15 mg/ml actin and 10 molar microtubules. Both actin and microtubules are either monomeric (i.e. G-actin and α and β- tubulin) or filaments. The relative size of the monomeric and polymeric pools depends on cell type and the cell's phase within the cell cycle. Both types of filaments are polar and dynamic, with + and - ends with different rates of polymerization, and turnover times for actin filaments and microtubules of about 6 and 10 minutes, respectively. The continuous input of energy provided by the ATP hydrolysis that accompanies polymerization maintains the dynamics. Filament length stays constant only under special conditions in which the rates of polymerization and depolymerization are equal (this phenomenon is particularly relevant for actin and is called treadmilling). Filament binding proteins can change filament dynamics.

The large number and concentration of different cytoskeletal proteins prohibit a complete simulation of the cytoskeleton. We construct an initial interconnected cytoskeleton with a fixed concentration of rigid rod filaments and start their dynamic evolution. The rods may represent various cytoskeletal filaments if we choose their diameter appropriately (8 nm and 24 nm respectively for actin filaments and microtubules). The length of the rods follows a uniform distribution. Each rod has six parameters that describe its location in space: Cartesian coordinates for one endpoint, the rod's length and two angles, for its orientation.

While constructing the network, we observe the following rules. Two rods cannot penetrate each other. Once two filaments are within a minimal distance of one another (soft core) a node forms at the point of closest approach and the two rods connect. Rods occupy the space between the nucleus and the cell surface. Special nodes denote points where a rod end reaches the surface of the nucleus (exit points) or the cell surface (entry points).

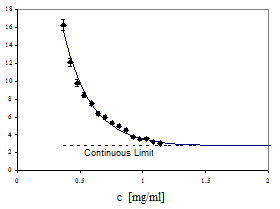
This minimum model is the starting point for our simulations (Shafrir et al., 2000). Depending on the particular cytoskeleton function we wish to study we elaborate the model. For example, we can place cross-linkers at the nodes. Special biased deposition rules for constructing the network can model bundling and stress fiber formation: if a filament lands within the soft core of a previously placed filament it aligns with it, forming bundles. Actin and microtubule binding proteins decorate the basic network. The minimal model can address fundamental questions. For example, we have considered a hypothetical signaling cascade consisting of a single molecule and the efficiency of its translocation to the nucleus (as measured by the first passage time, Figure V.11) via the following three mechanisms: (i) free unhindered diffusion through the cytoplasm, (ii) free diffusion in the presence of the cytoskeleton and (iii) quasi one-dimensional diffusion along the cytoskeletal tracks. Under reasonable assumptions about concentration and mechanical properties of the filaments, the third mechanism is the most efficient.

As a next step we will take include actin filament and microtubule polarity and biased diffusion along the macromolecular tracks. More important, the model can include a reasonable caricature of the dynamics of the cytoskeleton. Actin filaments grow or shorten by attaching or detaching G-actin monomers, which cannot bind to F actin without a bound cation (Mg²⁺, Ca²⁺) and a bound nucleotide (ATP or ADP). Thus the rate constants of actin polymerization are numerous (depending on the combination of G-actin, cations, especially Mg²⁺, Ca²⁺ and KCl, and nucleotides) and differ at the two ends (barbed or + and pointed or -) of the filament. The comprehensive intra-cellular automaton model of Dufort and Lumsden (1993), who studied the dynamics of the microfilament network revealed the complexity of a quantitative analysis of the actin cytoskeleton. They included the effect of profilin (a monomer sequestering protein) and gelsolin (filament capping protein). -actinin cross-linking of the filaments employed the empirical kinetics.

Fig. V.11. First passage time (FPT) to arrive from the cell surface to the nucleus by diffusing along interconnected discrete filaments, as a function of filament (IF-actin) concentration. The value of the FPT along the discrete model cytoskeleton converges to that in the continuous cytoplasm without obstacles (broken line). The heavy line illustrates how FTP increases if the discrete filaments obstruct free three-dimensional diffusion.

They simulated a volume of radius 0.6 µm for a short time while the typical size of cells is ~10 µm. However, their results indicate that if enough cross-linkers are available, the microfilament network globally interconnects, supporting our algorithm for the construction of the model cytoskeleton.

We will incorporate elements of the Dufort-Lumsden model in our simulations. We will model the association and dissociation between F-actin and the cross-linkers (initially -actinin) with rate constants from Meyer and Aebi (1990) (k+=3.0 (µMs) ^-1 and k-=3.0 s^-1 for the association and dissociation of F-actin and α actinin, respectively). We also allow for the polymerization and depolymerization of microfilaments, but instead of the 8 pairs of (on and off) rate constants that Dufort and Lumsden list (corresponding to all the combinations of G actin, cations (Mg²⁺, Ca²⁺), nucleotides (ATP, ADP) and barbed and pointed ends) we initially distinguish only the filament ends and average the corresponding four rates. Temporal changes in the network are our extension of the earlier simulations.

Our model cytoskeleton resides in a cell, in an environment with well-defined physical characteristics (i.e. viscosity). The filaments have physical attributes that we will have to incorporate into our model. This information will come from the experiments of other Consortium members.

The cytoskeleton is a complex network of actin filaments, microtubules and intermediate filaments. All of which (Pollard, 1984; Svitkina and Borisy, 1996; Goode et al., 2000) to interact with each other. A realistic model of the full cytoskeleton should incorporate these interactions. At present detailed modeling of these interactions is impossible because the relevant pathways are still too poorly characterized. Our eventual goal is to assemble the combined evidence into a coherent interaction network connecting the actin and tubulin cytoskeletons.