Organogenesis - Indiana University - The Biocomplexity Institute

Organogensis

VI.1 COORDINATORS
VI.2 PARTICIPANTS
VI.3 SUMMARY
VI.4 INTRODUCTION
VI.5 SPECIFIC AIMS
VI.6 BACKGROUND AND SIGNIFICANCE
VI.7 THEORETICAL FRAMEWORK

VI.8 PRELIMINARY RESULTS
VI.9 RESEARCH DESIGN AND METHODS
VI.10 RELATIONSHIP TO CYTOSKELETON (PROJECT 2) AND BIOLOGICAL NETWORKS (PROJECT 1)
VI.11 TIMELINE

< Previous | Page 9 of 27 | Next >

VI.7 THEORETICAL FRAMEWORK:

VI.7.i Overview:

Organogenesis involves many processes (e.g. cell-cell adhesion, cell-matrix adhesion, chemotaxis, mitosis, etc.). Our general modeling strategy is to select known mechanisms (i.e. specific quantitative models), which mimic individual experimental phenomena. Once we understand these mechanisms individually we combine them to develop more comprehensive models of morphogenesis. Finally, we look for novel effects and experimentally testable predictions.

Most of our modeling uses the Cellular Potts Model (CPM), but we also use other techniques when appropriate including simple, point-cell cellular automata.

VI.7.ii Cellular Potts Model:

VI.7.ii.a Energy Minimization Formalism:

The central element of the CPM is an energy minimization formalism to simulate the movement and properties of spatially extended cells undergoing cytoskeletally driven fluctuations. Extensive quantitative experiments have shown that it successfully reproduces the behavior of simple cell aggregates (Beysens et al., 1998; 2000; Mombach and Glazier, 1996; Mombach et al., 1995; Rieu et al., 2000; Upadhyaya et al., 2001).

fundamental entities in our model are individual cells. An effective energy E and "fields," e.g. the local concentrations of diffusants, conveniently describe their interactions, motion, differentiation and division. The effective energy mixes true energies, like cell-cell adhesion, and terms that mimic energies, e.g. the response of a cell to a chemotactic gradient. Given an effective energy we can calculate the resulting cell motion, since differences in energy produce forces, 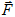. Since cells in tissues move in an extremely viscous environment, the velocity of the center of mass of the cell, v, not acceleration is proportional to force, with an effective cell mobility, m. Thus 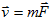; i.e.,

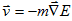(VI.1)

Equation (VI.1) implies that cells move to minimize their total effective energy. In what follows we discuss the various energy contributions and fields we incorporate in our simulations.

We can implement equation (VI.1) in a simulation in a number of ways, using center, vertex, boundary or finite element methods (Graner, 1993, Graner and Sawada, 1993). Up to the accuracy of our approximations all methods yield the same results. We have found that the CPM, a cellular automaton derived from the Potts model of statistical physics, optimizes tradeoffs between efficiency, complexity of code and accuracy. (Graner and Glazier, 1992; Glazier and Graner, 1993; Jiang et al., 1998; Marée, 2000). The CPM superimposes a lattice on the cells, with each lattice site associated to an index. The value of the index at a lattice site is σ if the site lies in cell σ (Srolovitz et al., 1984; Grest et al., 1988; Glazier, 1989). Finite connected domains in the lattice represent cells. Cell shape changes correspond to domain deformations. Similarly we discretize any auxiliary fields and evolve them according to appropriate equations. The parameters of each cell evolve according to the equations we define for their internal states (Section VI.7.i.c).

VI.7.ii.b Cell Adhesion:

We can describe the net interaction between two cell membranes by an effective cell-type dependent binding energy per unit area, J_τ,τ&prime, where τ is the type of the cell on either side of the link, which incorporates both specific (e.g. integrins, cadherins) and nonspecific interactions (e.g. elastic effects due to cell deformations, Drasdo and Forgacs, 2000) as measured with laser tweezers (Sato-Maeda et al., 1994), compression apparatus (Foty et al., 1996), or micropipette aspiration techniques (Merkel et al., 1999). In the CPM the effective cell-cell interaction energy is:

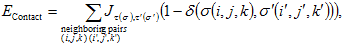(VI.2)

where the Kroneker δ, (δ(σ,σ′)=0 if σ≠σ′ and δ(σ, σ′)=1 if σ= σ′), ensures that only surface sites between neighboring cells contribute to the cell adhesion energy.

Based on energy minimization under differential adhesion (DAH) Steinberg (1963) predicted that in an aggregate of two cell types, if the heterotypic energy is greater than the homotypic, the lowest energy configuration has the less cohesive cell type completely surrounding a sphere of the more cohesive cell type. Many assays have observed this classic cell sorting (Steinberg and Takeichi, 1994). Complications arise because the cell adhesion molecules may change both in quantity and identity (Bozzaro and Ponte, 1995). We model all such changes as variations in cell-specific adhesivity. Cell-cell interactions are adhesive, thus the coupling energy is negative (Upadhyaya, 2001), J_τ,τ′<0. for the surface energy term, the membrane breaks up to try to maximize its surface areas (and hence minimize its energy).

VI.7.ii.c Cell Volume, Mitosis and Apoptosis:

At any time t, a cell, of type, τ, has a volume v(σ,t) and surface area s(σ,t). Since cell volume can fluctuate, e.g., due to changes in osmotic pressure, we describe the cell volume in terms of an effective volume elasticity, λ and target volume v_target(σ,t). We define a membrane elasticity, λ′, and a target surface area s_target(σ,t):

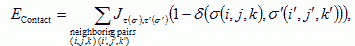(VI.3)

When a cell grows, both v(σ,t) and s(σ,t) increase, otherwise vtarget(t) and starget(t) are constant. Mitosis occurs either when the cell reaches a fixed, type-dependent volume, or when the ratio between cell surface area and cell volume reaches a critical value (Drasdo, 1996). For a specific form see Drasdo and Forgacs (2000). We create two daughters with their plane of separation along the parent cell's longest axis and new target areas v_target/2, based on experiments that show well-defined orientation of cleavage planes with mitotic spindles aligned according to the positions of neighboring cells (See Project 2, Subproject 2) (White and Borisy, 1983). We can simulate apoptosis simply by setting the cell's target volume to zero.

This simple model reproduces the observed cell arrangements in a variety of plant tissues (Mombach et al., 1993) and avascular tumors (Stott et al., 1999; Drasdo et al., 1995).

VI.7.ii.d Extracellular Matrix:

We model ECM, liquid medium and solid substrates, as cells with the property that their target area always tracks their current area. ECM is similar to a secreted signaling molecule except that the secreted material does not diffuse. If a cell secretes a unit of ECM, the ECM's target area increases by one unit. Similarly if a cell absorbs a unit of ECM, the ECM target area decreases by one. If the ECM is solid, then local concentrations of ECM cannot fluctuate or move, if liquid, it behaves exactly like a normal cell. We must define the interaction energy between each cell type and the ECM.

VI.7.ii.e Cell Polarity:

The distribution of cell adhesion molecules is typically nonuniform along the cell membrane, due to cell polarity. We simulate polarity by defining an orientation vector for each cell and allowing J to vary as a function of the position on the cell surface with respect to the orientation vector. Extremely polar cells characterized by their apical and basal surfaces (Bozzaro and Ponte, 1995; Kuspa et al., 1992; Roberson et al., 1980), contact their neighbors along the lateral part of their membranes to form epithelial sheets. The sheet has a local spontaneous curvature, c_σ.σ at site σ(Lipowsky, 1991) determined exclusively by the preferred shape of the individual cell at σ. The curvature of a surface at point σ is defined as 1/r_σ , where r is the local radius of curvature. Bending the sheet distorts the membrane, costing energy (Drasdo and Forgacs, 2000):

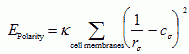(VI.4)