Organogenesis - Indiana University - The Biocomplexity Institute

Organogensis

VI.1 COORDINATORS
VI.2 PARTICIPANTS
VI.3 SUMMARY
VI.4 INTRODUCTION
VI.5 SPECIFIC AIMS
VI.6 BACKGROUND AND SIGNIFICANCE
VI.7 THEORETICAL FRAMEWORK

VI.8 PRELIMINARY RESULTS
VI.9 RESEARCH DESIGN AND METHODS
VI.10 RELATIONSHIP TO CYTOSKELETON (PROJECT 2) AND BIOLOGICAL NETWORKS (PROJECT 1)
VI.11 TIMELINE

< Previous | Page 10 of 27 | Next >

VI.7.ii.f Membrane Fluctuations:

How do cells move? In mixtures of liquid droplets, the thermal fluctuations of the droplet surfaces cause diffusion (Brownian motion) leading to energy minimization. Cytoskeletally driven cell membrane ruffling of a few micrometers (µm) has no need to be thermal and cell and tissue dynamics might depend sensitively on details of the fluctuations spectrum. The simplest assumption is that an effective temperature, T, drives cell membrane fluctuations. We can describe these fluctuations statistically using Monte-Carlo Boltzmann dynamics (Metropolis, 1953), where T defines the size of the typical fluctuation. If a proposed change in configuration produces a change in effective energy, ΔE, we accept it with probability:

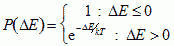(VI.5a)

...where k is a constant converting T into units of energy.

The formation and breakage of CAM bonds is dissipative. Therefore Hogeweg et al. corrected the classical Boltzmann index evolution dynamics to include an explicit dissipation (Hogeweg, 2000):

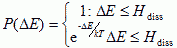(VI.5b)

...where, H_diss, represents the dissipation costs of deforming a boundary.

For realistic values of the simulation parameters measured for Hydra cell aggregates, the simulated diffusion constants have the correct value (Rieu et al., 2000). In chick retina, the spectrum of velocities of a single pigmented cell in a neural cell aggregate is identical to that of a simulated cell (Mombach and Glazier, 1996).

VI.7.ii.g Correlated Cell Motion:

Once a cell begins to move in a given directions, it tends to continue because forming or destroy a leading edge takes time. While persistence times vary greatly, for limb mesenchymal cells a reasonable time is one minute (Upadhyaya et al., 2000). We can include a constraint on the cell velocity of our usual form to enforce persistence in our simulations:

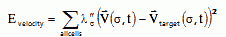(VI.6)

...where 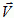is the instantaneous velocity of a cell due to an index change, V_target is the velocity of the cell averaged over a time interval (or at the previous time step) and λ″ is the correlation strength. If λ″=0 the cells execute Brownian random motion and if λ″ is very large they move continuously in one direction at fixed velocity like keratocytes.

VI.7.ii.h Chemotaxis:

Chemotaxis requires additional fields to describe the local concentrations 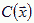of the molecules diffusing in extracellular space (or, in the presence of gap junctions, through cells as well). Let the molecule's diffusion constant be d, its decay rate Γ, and let it be secreted or absorbed at the surface of cells in a history dependent way, 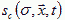. To model a specific form for s_c requires experimental measurement of the concentrations of diffusing morphogens in the tissue. The equation for the field then is (Levine et al., 1996; Hofer et al., 1995):

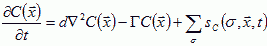(VI.7)

We describe the cell's response to the chemotactic field by an effective chemical potential, µ(σ), which may be time dependent, e.g. in a refractory period µ(σ), will be nearly 0 or the cell may adapt, in which case the value of µ(σ) depends on the cell's previous exposure to C described by a set of ODEs. µ(σ)>0 yields repulsion, and µ(σ)<0 attraction. The effective chemical energy, which we incorporate into the CPM is:

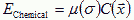(VI.8)

We can measured µ(σ) experimentally in dynamic flow-through experiments (H. Levine, personal communication, 2001). The cell executes a biased random walk, which averages to directed motion in the direction of the gradient:

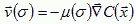(VI.9)

which has the same form as equation (VI.1), justifying our energy treatment.

VI.7.ii.i Pattern Formation by Reaction-Diffusion:

Besides treating the motion of individual cells we must simulate the diffusion of morphogens, chemoattractants and chemorepellants. Turing (1952) introduced the classic reaction-diffusion equation model of differentiation to treat pairs of continuous fields rather than individual cells. His formalism carries over to the CPM. If A and B are diffusing morphogens, which evolve like the diffusants in chemotaxis (Turing, 1952):

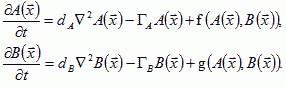(VI.10)

A is excitatory if 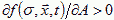and inhibitory if 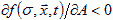. If A is excitatory and B inhibitory and B diffuses faster than A, d_A<d_B, then an initial uniform distribution of A and B is unstable and the concentration field will evolve into domains (Turing, 1952). Cells, instead of moving, can change their parameters, e.g. their membrane adhesivities and elasticities, in response to A and B, as a function, h, of the surface concentrations of the chemoattractants, where h is defined by a model for the internal state of the cell:

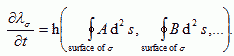(VI.11)

VI.7.ii.j Modeling the Internal State of the Cell:

The closest link between experimental molecular biology and computation is at the level of the modeling of the internal state of the cell. Modeling the internal state of a cell is necessary to understand how cells differentiate. The program of Project 1 and the genetic screening described in this section will generate a great deal of data on the regulatory mechanisms that determine the internal cell state.

If cells differentiate primarily as a result of their history and not due to positional signals, then the cell carries a set of internal variables describing its state, which evolve according to a set of internally defined ordinary differential equations. These states are general logic gates formed by biochemical reaction networks (Arkin and Ross, 1994). The necessary signal to switch on a gene probably depends on a biochemical reaction network (BRN).

On the multicellular level a gradient of a diffusible morphogen based on purely reaction-diffusion mechanisms persists only in small tissues ~1 mm, otherwise the time required for diffusive exchange of molecules is too long. In larger organisms and tissues, particular genes have to be activated in response to signals, setting off a gene cascade, which requires autocatalytic activation of genes (Meinhardt, 1978). More complex interactions allow the space-dependent activation of several genes under the influence of a single gradient (Meinhardt, 1978).

Simulations of stochastic gene expression (McAdams and Arkin, 1997) based on studies of biochemical reaction networks by Arkin and Ross (1994) suggest that an activated promoter produces variable numbers of proteins in short bursts at random time intervals. As a result, the time between successive events in regulatory cascades can differ greatly across a cell population.

Many molecules that control genetic regulatory circuits act at extremely low intracellular concentrations in inhomogeneous environments. Resultant fluctuations (noise) in the reaction rates can cause large random variation in rates of development, morphology and the instantaneous concentration of each molecular species in each cell. For regulatory reliability cells use redundancy in genes as well as redundancy and extensive feedback in regulatory pathways (Project 1). We shall model such noisy processes in inhomogeneous environments using Monte Carlo techniques (Krauss et al., 1996).

To model spatial variations of chemical concentration arising from the BRN inside the cell we need to incorporate the relevant boundary conditions at the cell membrane and nucleus (Hentschel and Fine, 1994; 1996). We can find these heterogeneous concentrations by solving numerically the relevant reaction-diffusion equation subject to biologically plausible conditions for the fluxes at the evolving free boundary of the tissue. Experiments must determine their functional form and magnitude.