Organogensis

VI.1 COORDINATORS
VI.2 PARTICIPANTS
VI.3 SUMMARY
VI.4 INTRODUCTION
VI.5 SPECIFIC AIMS
VI.6 BACKGROUND AND SIGNIFICANCE
VI.7 THEORETICAL FRAMEWORK

• VI.7.i Overview
• VI.7.ii Cellular Potts Model
  • VI.7.ii.a Energy Minimization Formalism
  • VI.7.ii.b Cell Adhesion
  • VI.7.ii.c Cell Volume, Mitosis and Apoptosis
  • VI.7.ii.d Extracellular Matrix
  • VI.7.ii.e Cell Polarity
  • VI.7.ii.f Membrane Fluctuations
  • VI.7.ii.g Correlated Cell Motion
  • VI.7.ii.h Chemotaxis
  • VI.7.ii.i Pattern Formation by Reaction-Diffusion
  • VI.7.ii.j Modeling the Internal State of the Cell
  • VI.7.ii.k Model of Innervation
  • VI.7.ii.l Point Cellular Automata Simulations

VI.8 PRELIMINARY RESULTS
VI.9 RESEARCH DESIGN AND METHODS
VI.10 RELATIONSHIP TO CYTOSKELETON (PROJECT 2) AND BIOLOGICAL NETWORKS (PROJECT 1)
VI.11 TIMELINE

< Previous | Page 11 of 27 | Next >

VI.7.ii.k Model of Innervation:

How do neurons innervate a developing limb to create a topographic map by layers of neurons? The actual equations depend on the biology. Consider the interaction of two types of diffusible molecules: (1) a chemoattractant, which the target cells release at rate J_target, has diffusion constant D_target, and spatial concentration 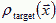and (2) a chemoattractant, which the axonal growth cones release at rate J_cone, has diffusion constant D_cone, and concentration 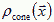. More complex models can include chemorepellants to control debundling. For two diffusive fields the equations for the concentration gradients are,

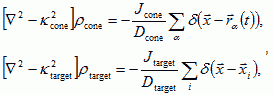(VI.12)

where r_α(t) is the position of growth cone α at time t, and the target cells and growth cones behave like point sources. Both chemoattractants degrade in the extracellular space, resulting in finite diffusion lengths 1/Κ_target, and 1/Κ_cone. Nerve fibers move up the gradients of the chemoattractants at rates proportional to the gradients, but are also move randomly due to variations in the ECM and the fluctuations of the growth cone. Thus the total response of the growth cone is:

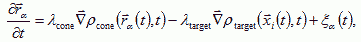(VI.13)

where λ_cone, and λ_target are the growth rates of the axon towards the cone and target chemoattractant gradients; and ξ_α(t) are the random growth cone movements.

VI.7.ii.l Point Cellular Automata Simulations:

When the number of cells under study is too large to use the CPM, we can reduce computational demands by representing each cell as a point particle and treating continuum fields as arrays of points. A cellular automaton is a dynamical system defined on a regular lattice with a finite number of states assigned to each cell of the lattice. It is discrete in space, time, and state, whereas most systems of interest in biology are continuous. Cellular automata (CA) nonetheless have been used to model biological processes as varied as predator-prey dynamics in fish populations (Dewdney 1988; Ermentrout and Edelstein-Keshet, 1993), bacterial colony growth (Kreft et al., 2001), and pacemaker activity in cardiac tissue (Winfree et al., 1985; Kaplan et al., 1988). The applicability and power of such models lies in the surprisingly rich array of complex behaviors and spatial patterns arising from the interaction of components that follow simple rules (Wolfram 1983, 1994, 2002).

Like all CA, LGCA employ a regular, finite lattice and include a finite set of particle states, an interaction neighborhood and local rules which determine the particles' movements and transitions between. LGCA differ from traditional CA by assuming particle motion and an exclusion principle. The connectivity of the lattice fixes the number of allowed velocities for each particle. For example, a nearest-neighbor square lattice has four non-zero allowed velocities. The velocity specifies the direction and magnitude of movement, which may include zero velocity (rest). In a simple exclusion rule, only one particle may have each allowed velocity at each lattice site. Thus, a set of Boolean variables describes the occupation of each allowed particle state: occupied (1) or empty (0). Each lattice site can then contain from zero to five particles.

The transition rule of an LGCA has two steps. An interaction step updates the state of each particle at each lattice site. Particles may change velocity state, appear or disappear in any number of ways as long as they do not violate the exclusion principle. For example, colliding particles may be deterministically assigned to mirroring or adjacent velocity channels, or the assignment may be random. In the transport step, cells move synchronously in the direction and distance their velocity state specifies. Synchronous transport prevents particle collisions which would violate the exclusion principle (other models define a collision resolution algorithm). LGCA models are specially constructed to allow parallel synchronous movement and updating of many particles.