Note: this page is a mirror of http://www.nd.edu/~lcls/compucell/.

CompuCell

CompuCell is a software framework for multimodel simulations of biocomplexity problems. It has been developed as an ongoing project for the Interdisciplinary Center for the Study of Biocomplexity at the university of Notre Dame (http://www.nd.edu/~icsb/).

By biocomplexity we mean the study of complex structures and behaviors that arise from the interaction of biological (biophysical!) entities (molecules, cells, organisms). The complex interplay of physical and chemical processes give rise to a great variety of spatial and temporal structures, resulting in rich complexity of even the simplest biological phenomena.

CompuCell currently uses a combination of "extended Potts model" for cell sorting and clustering, and "Schnakenberg Reaction Diffusion" equations to establish the underlying chemical field to which cells respond and form typical patterns found in such biological systems as a growing chicken limb. We provide an example (and results) showing how the system can be used to simulate the formation of patterns that resemble the growth of limb in a chicken embryo. The limb-growth-model is described in greater detail in the "Examples" section. The animated gif on this page (see Movies section) shows the result of simulations carried out with CompuCell.

(Written: July 2, 2002, by Rajiv Chaturvedi: rchaturv@nd.edu)

Download

CompuCell is freely distributed under GPL via SourceForge. Please visit the CompuCell Project Site for the latest downloads and CVS access. Also, please make sure you visit the CompuCell Wiki, an invaluable source to communicate directly with the developers of CompuCell.

Documentation

Below are some helpful resources related to CompuCell. Some may be slightly out of date, but the general information should still be useful.

• Overview of the Actual Keywords, Default Values and Types (TEXT) (Trevor M. Cickovski)
• User Guide 1.6 Beta: CompuCell: A Software Framework For Multimodel Simulations Of Biocomplexity Problems (PS) (PDF) (HTML) (Jesus A. Izaguirre, Rajiv Chaturvedi, Trevor M. Cickovski and Chengbang Huang)
• A Front End Design For Simulation Engines (PS) (PDF) (HTML) (Jesus A. Izaguirre with Trevor M. Cickovski)
• Design Document For CompuCell and BioLogo (PS) (PDF) (HTML) (Jesus A. Izaguirre with Trevor M. Cickovski)

3D Examples

3D simulations of limb bud

3D limb bud simulations. Submodels used: Potts for cell dynamics, RD for TGF-beta, Cell state automaton for RO, ROC, medium states, Fibronectin ODE's. RD prepattern is shown at right. Initial number of cells ~2500. Iterations = 600, time~12 hours. RD Simulation Movie can be viewed HERE. NOTE: This is a large animated GIF! (below) The change from one bone to two bones. For this simulation, the ratio between width and length is 2:7(2 in y-direction and 7 in x-direction), and the actual length in x-direction is taken to be 3.0. The grid size of the whole domain is 20 by 70 by 210. The parameters for Schnakenberg kinetics are: a=0.017, b=1.015, d=7.1 Ratio 2:7, Length=3.0, diffusion=7.1

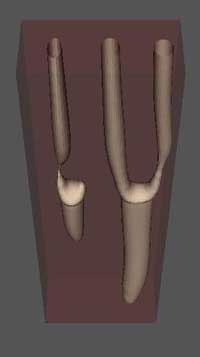
2D Examples

Schnakenberg Equation
Example 1: Limb bud growth in chicken

Gamma: 2 steps	Gamma: 3 steps	Gamma: linear

Fibronectin Simulations

Moving Potts Simulations

CompuCell1.5 100	Cells CompuCell1.6 100 Cells
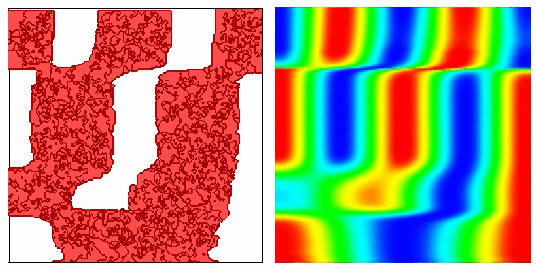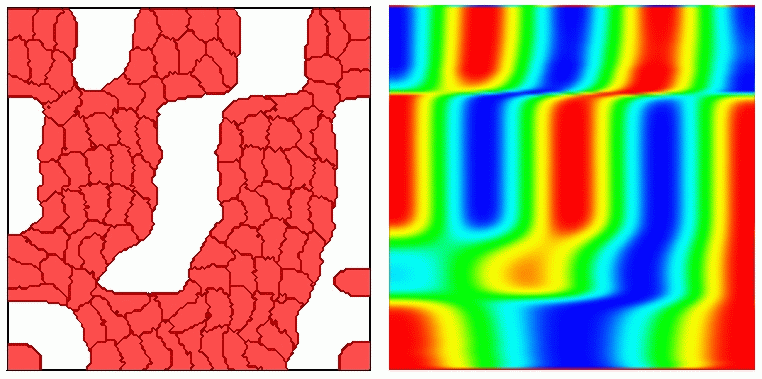Configuration	Configuration

Movies

Fibronectin Movie #1
Fibronectin Movie #2
Moving Potts with Boundary - 100 cells
2-D simulation with Fribronectin and mitosis (initial height: one 6th of total)

For Source Code or Questions Contact:

CompuCell Team
Laboratory for Computational Life Sciences
Department of Computer Science and Engineering
University of Notre Dame
325 Fitzpatrick Hall of Engineering
Notre Dame, Indiana 46556 USA
compucell@cse.nd.edu

Acknowledgements

This research is supported in part by
a National Science Foundation Biocomplexity grant PHY-0083653
a National Science Foundation ACI CAREER award ACI 01-35195
and the Center For Applied Mathematics at the University of Notre Dame