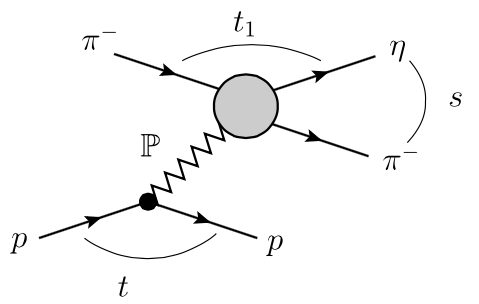
We present the model published in [Rod18a]
concerning the analysis of both processes $\pi^- p \to \pi^- \eta p$ and $\pi^- p \to \pi^- \eta' p$.
We report here only the main features of the model.
The partial waves were extracted by the COMPASS collaboration using a 190 GeV $\pi^-$ beam
and published in [COM14a].
The code can be downloaded in Resources section.
The two channels are $i=1,2$ for $\eta\pi$ and $\eta'\pi$ respectively.
$J=1,2$ for the $P$- and $D$-wave.
$s$ is the $\eta\pi$ invariant mass squared.
The intensities and phases displayed on the figures are
\begin{align}
I^J_i(s) & = p_i(s) |a^J_i(s)|^2, &
\phi_i(s) &= \arg[a^1_i(s)] - \arg[a_i^2(s)]
\end{align}
The momentum of the particles are $p^2_{1,2}(s) = \lambda(s,m_{\eta^{(')}}^2,m_\pi^2)/4s$
with $\lambda(a,b,c) = a^2+b^2+c^2-2(ab+bc+ca)$.
The amplitudes are the ratio of a numerator $n_i(s)$ and a denominator $D^J(s)$:
\begin{equation}
a^J_i(s) = q^{J-1} p_i^J \, \sum_{k=1,2} n^J_k(s) \left[ {D^J(s)}^{-1} \right]_{ki}\,,
\end{equation}
The break-up momentum between the exchange and the beam is $q^2 = \lambda(s,t,m_\pi^2)/4s$
with $t = -0.1$ GeV$^2$.
The numerator $n_k^J(s) = \sum_{n=0}^3 a_{n,k}^{J} T_n ( \frac{s}{s+s_0} )$ is expanded
in Chebychev polynomials $T_n$
with $s_0=1$ GeV$^2$.
The denominator is given by a $K$-matrix and a Chew-Mandelstam phase-space:
\begin{equation}\label{eq:Dsol}
D^J_{ki}(s) = \left[ {K^J(s)}^{-1}\right]_{ki} - \frac{s}{\pi}\int_{s_{i}}^{\infty}ds'\frac{\rho N^J_{ki}(s') }
{s'(s'-s)}.
\end{equation}
$s_{1,2} = (m_\pi+m_{\eta^{(')}})^2$ is the threshold of channel $i$.
The Chew-Mandelstam is diagonal in the channel space and is given by (with $s_L$ = 1 GeV$^2$)
\begin{align}
\rho N^J_{ki}(s') &= \delta_{ki} \,\frac{\lambda^{J+1/2}\left(s',m_{i}^2,m_\pi^2\right)}
{\left(s'+s_L\right)^{2J+3}}.
\end{align}
The $K$-matrix features two poles in the $D$-wave and one pole in the $P$-wave.
In both waves, a linear background complement the pole(s):
\begin{align}
K^J_{ki}(s) &= \sum_{R=1,2} \frac{g^{J,R}_k g^{J,R}_i}{m_R^2 - s} + c^J_{ki} + d^J_{ki} \, s
\end{align}
The parameters are given in the supplemental material of the publication [Rod18a].
The model is compared to the data on the figure:
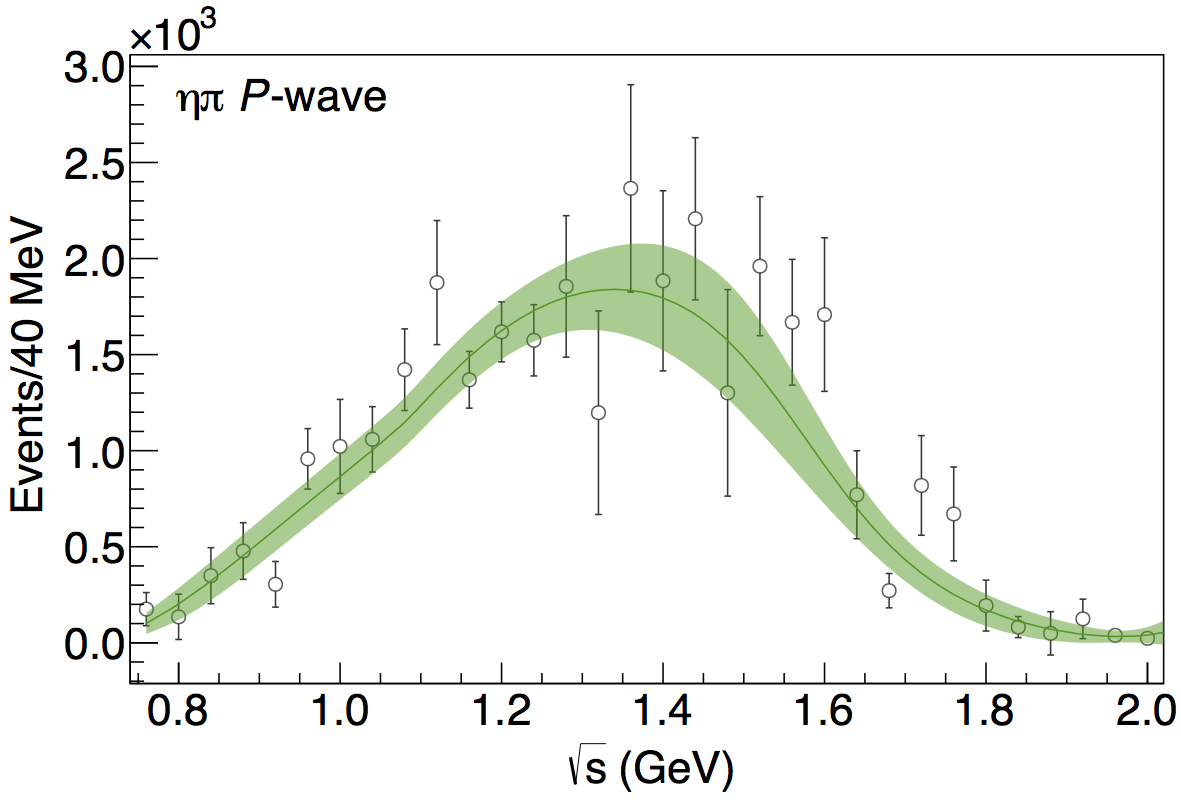
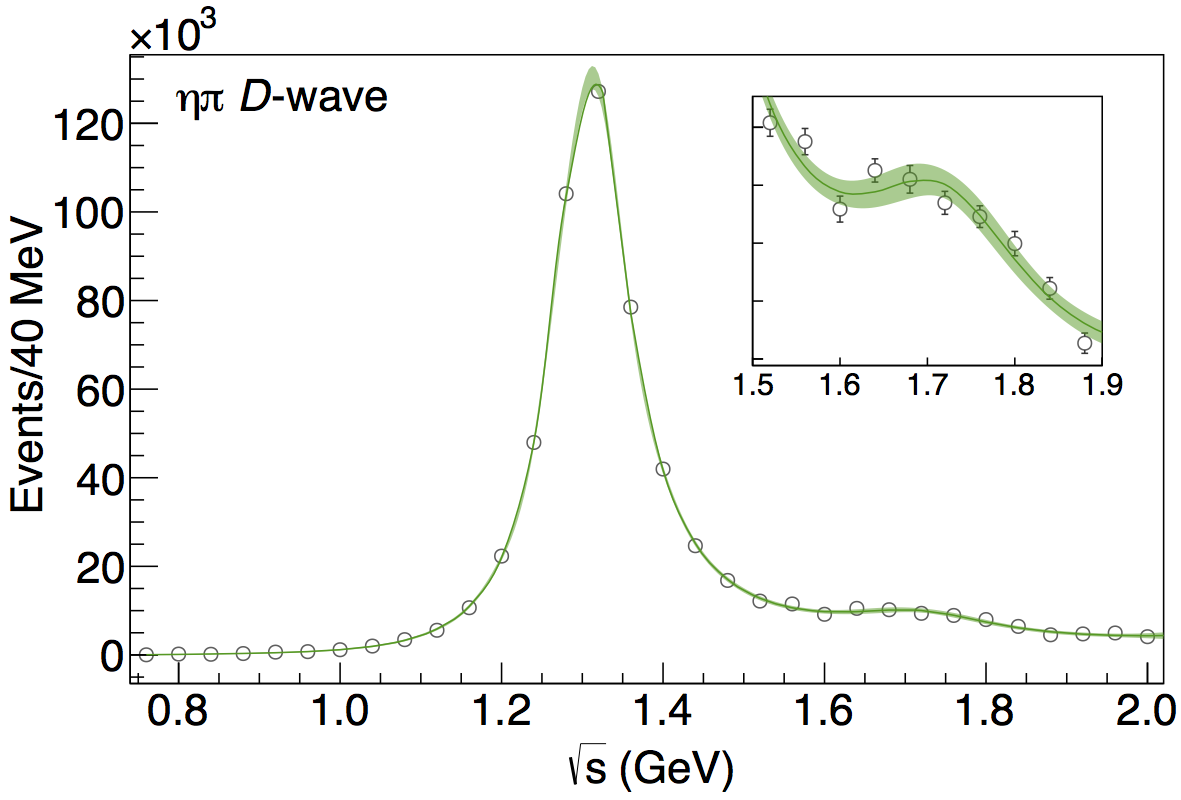
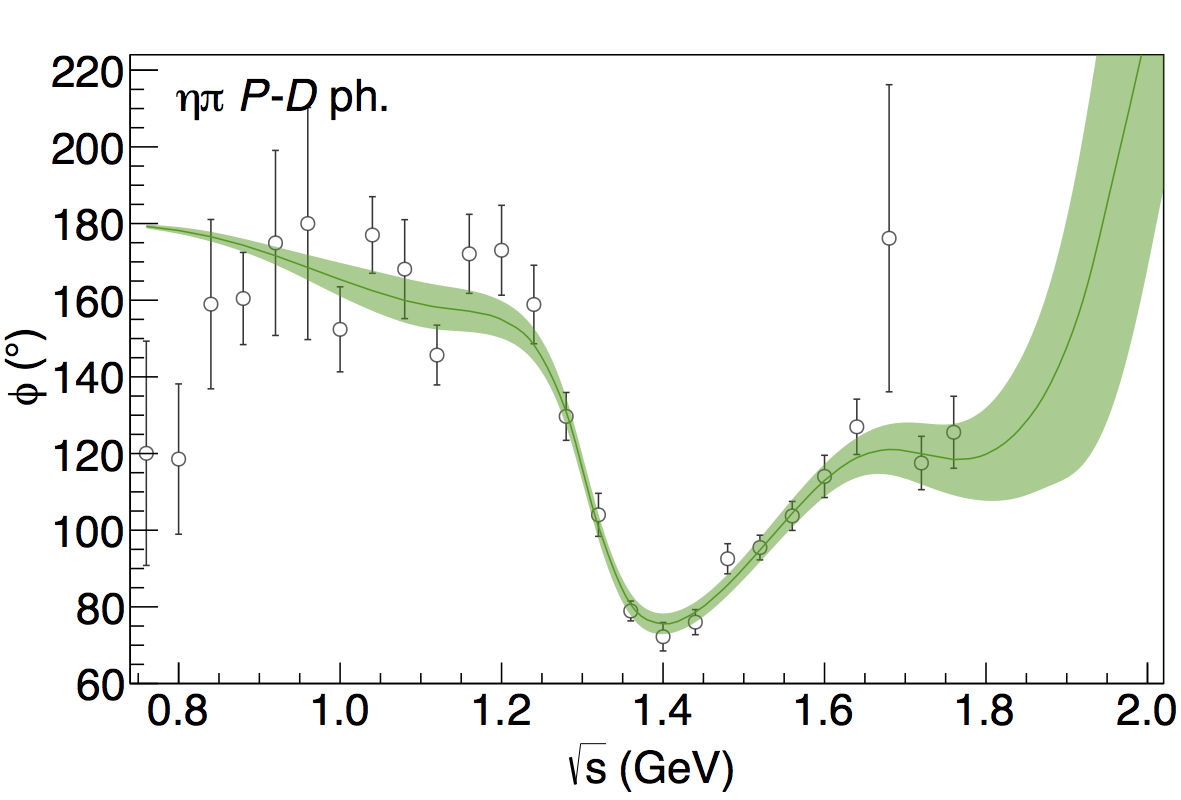
The pole location on the second Riemann sheet are displayed on the figure:
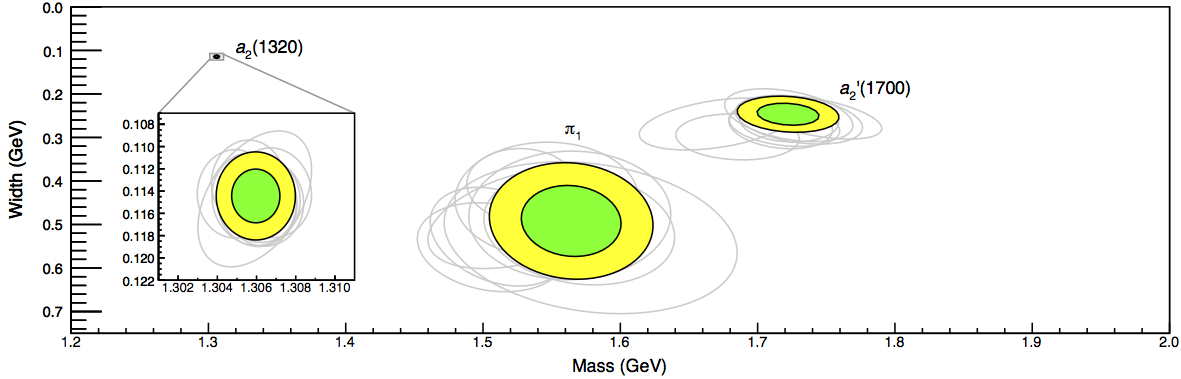
| Pole | Mass (MeV) | Width (MeV) |
| $a_2(1320)$ | $1306.0 \pm 0.8 \pm 1.3 $ | $114.4 \pm 1.6 \pm 0.0$ |
| $a_2'(1700)$ | $1722 \pm 15 \pm 67 $ | $247 \pm 17 \pm 63$ |
| $\pi_1(1600)$ | $1564 \pm 24 \pm 86 $ | $492 \pm 54 \pm 102$ |
References
[COM14a]
COMPASS Collaboration,
``Odd and even partial waves of $\eta\pi^-$ and $\eta'\pi^-$ in $\pi^- p \to \eta^{(')}\pi^- p$ at 191 GeV/c,''
Phys. Lett. B740 (2015) 303.
[Rod18a]
A. Rodas, A. Pilloni, M. Albaladejo, C. Fernandez-Ramirez, A. Jackura,V. Mathieu,
M. Mikhasenko, J. Nys, V. Pauk, B. Ketzer and A. P. Szczepaniak (JPAC)
``Determination of the pole position of the lightest hybrid meson candidate,''
arXiv:1810.04171 [hep-ph]
Resources
- Publications: [Rod18a]
- C/C++: C/C++ files in a .zip
- Input file: param-Kmatrix.txt
- Output files: chew1.txt , chew1.txt , amp1.txt , amp2.txt , results.txt ,
- Contact persons: Arkaitz Rodas, Alessandro Pilloni
- Last update: December 2018
- param-Kmatrix.txt:
This input file include the $K$-matrix parameters in the format:
- $a_0^{P, \eta}$, $a_1^{P, \eta}$, $a_2^{P, \eta}$, $a_3^{P, \eta}$
- $a_0^{P, \eta'}$, $a_1^{P,\eta'}$, $a_2^{P, \eta'}$, $a_3^{P, \eta'}$
- $a_0^{D, \eta}$, $a_1^{D, \eta}$, $a_2^{D, \eta}$, $a_3^{D, \eta}$
- $a_0^{D, \eta'}$, $a_1^{D, \eta'}$, $a_2^{D, \eta'}$, $a_3^{D, \eta'}$
- $c^P_{\eta,\eta}$ $c^P_{\eta,\eta'}$ $c^P_{\eta',\eta'}$
- $c^D_{\eta,\eta}$ $c^D_{\eta,\eta'}$ $c^D_{\eta',\eta'}$
- $d^P_{\eta,\eta}$ $d^P_{\eta,\eta'}$ $d^P_{\eta',\eta'}$
- $d^D_{\eta,\eta}$ $d^D_{\eta,\eta'}$ $d^D_{\eta',\eta'}$
- $g^{P,1}_{\eta}$ $g^{P,1}_{\eta'}$ $m^2_{P,1}$
- $g^{P,2}_{\eta}$ $g^{P,2}_{\eta'}$ $m^2_{P,2}$
- $g^{D,1}_{\eta}$ $g^{D,1}_{\eta'}$ $m^2_{D,1}$
- $g^{D,2}_{\eta}$ $g^{D,2}_{\eta'}$ $m^2_{D,2}$
- chew1.txt and chew1.txt:
Chew-Mandelstam for the $P$- and $D$-wave in the format:
$m_{\eta\pi}$, Re[$CM(\eta)$], Im[$CM(\eta)$], Re[$CM(\eta')$], Im[$CM(\eta')$] - amp1.txt and amp2.txt:
Amplitudes for the $P$- and $D$-wave in the format:
$m_{\eta\pi}$, Re[$A(\eta)$], Im[$A(\eta)$], Re[$A(\eta')$], Im[$A(\eta')$] - results.txt:
The intensities and phase difference in the format:
$m_{\eta\pi}$, $I^1_\eta$, $I^1_{\eta'}$, $I^2_\eta$, $I^2_{\eta'}$, $\phi_\eta$, $\phi_{\eta'}$
- main.c:
Read the $K$-matrix parameters and print the results in files.
- partial-waves.c:
- Ampl: return the amplitudes
- invKmatrix: return the inverse of the $K$-matrix
- chewM.c:
- chewM_c: return the Chew-Mandelstam
- numCM_c: return the numerator of the Chew-Mandelstam
- intCM_c: return the integrand of the Chew-Mandelstam
- intCM_re and intCM_im: return the real and imaginary part of the integrand
- modules.c:
- lam: return $\lambda(a,b,c)$
- ChebyPol: return the Chebyshev polynomial
- simpson and int_adaptsimpson: adaptative Simpson method for integration
- print_c: print a complex number