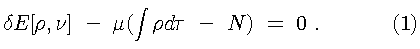
For many years wave function functional theory (Schrödinger theory) has been the method of choice when performing electronic structure calculations on chemical systems. However, within the last few years, density functional theory has experienced a rise in its popularity for calculating structures and properties of chemical systems. The need to include electron-correlation in calculations on large chemical systems and the discovery of new and more accurate approximations to the exchange-correlation energy density functional has contributed to the increased popularity of density functional theory. Not only does density functional theory (DFT) provide computational advantages over wave function functional theory (WFT), but quantities of interest to chemists (such as electronegativity, hardness, softness, reactivity indices, etc) are readily defined.
Density functional theory is equivalent to solving Schrödinger's equation and is, therefore, an exact theory for describing the electronic structure and properties of matter. An important difference between DFT and WFT is the principle quantity of interest. In DFT this quantity is the electron density which, unlike the wave function, is an observable. As a result, quantities not readily accessible through WFT are conveniently defined. The computational advantage of DFT originates with the fact that the electron density has three spatial coordinates, regardless of the number of electrons in the chemical system. Thus, DFT allows the calculation of structures and properties of molecules with a couple hundred atoms, a feat not generally possible with high-level WFT methods.
In 1964 the perception of density functional theory was forever changed. That year, Hohenberg and Kohn provided the long sought after proof that density functional theory is in fact an exact theory for describing the electronic behavior of matter. This was accomplished by proving the following remarkable theorem: There exits a variational principle in terms of the electron density which determines the ground state energy and electron density. Further, the ground state electron density determines the external potential, within an additive constant.
This states that the ground state electron density, as obtained from the Hohenberg-Kohn variational principle, uniquely determines the ground state properties of the system of interest. The electron density is obtained from the variational principle
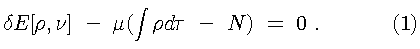
Here
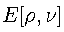 is the ground state energy, as a functional of both the electron
density
is the ground state energy, as a functional of both the electron
density
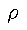 and external potential
and external potential
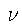 (the nuclear-electron attraction potential in many cases),
(the nuclear-electron attraction potential in many cases),
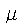 (the chemical potential) is a Lagrange multiplier introduced to
preserve the number of particles and N is the number of
electrons. For emphasis, we now explicitly denote the
functional dependence of the energy on the external potential.
The solution of the resulting Euler-Lagrange equation
(the chemical potential) is a Lagrange multiplier introduced to
preserve the number of particles and N is the number of
electrons. For emphasis, we now explicitly denote the
functional dependence of the energy on the external potential.
The solution of the resulting Euler-Lagrange equation
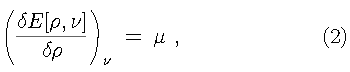
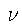 on the functional derivative implies that
on the functional derivative implies that
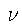 is kept fixed when performing the functional derivative with
respect to
is kept fixed when performing the functional derivative with
respect to
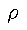 .
Equation [2] is the DFT counterpart to the Schrödinger
equation. The functional for the ground state energy can be
partitioned
.
Equation [2] is the DFT counterpart to the Schrödinger
equation. The functional for the ground state energy can be
partitioned
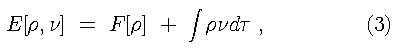
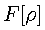 is a universal functional of
is a universal functional of
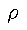 .
This universal functional contains kinetic and potential energy
contributions,
.
This universal functional contains kinetic and potential energy
contributions,
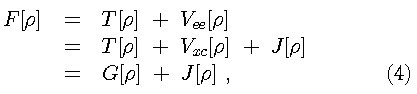
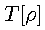 is a universal functional for the kinetic energy,
is a universal functional for the kinetic energy,
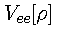 is a universal functional for the electron-electron repulsion
energy and
is a universal functional for the electron-electron repulsion
energy and
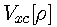 is a universal functional of the exchange-correlation energy.
Unfortunately, the exact forms of
is a universal functional of the exchange-correlation energy.
Unfortunately, the exact forms of
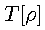 and
and
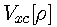 are not known. For this reason Eqs. [1] and [2] are not used in
practical applications of density functional theory. However
this formal development of density functional theory does
provide important relationships, which lead to useful
expressions for properties of chemical interest.
are not known. For this reason Eqs. [1] and [2] are not used in
practical applications of density functional theory. However
this formal development of density functional theory does
provide important relationships, which lead to useful
expressions for properties of chemical interest.
A practical description of density functional theory was given
by Kohn and Sham, just one year after the momentous
Hohenberg-Kohn paper. The Kohn-Sham implementation is based
upon an orbital-density description of DFT which removes
the necessity of knowing the exact form of
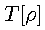 .
They proposed focusing on the kinetic energy of a
non-interacting system of electrons as a functional of a set of
single-particle orbitals which give the exact density. Levy has
since presented a constrained search formulation of Kohn-Sham
theory in which the kinetic energy of a non-interacting system
of electrons is minimized with respect to a set of
single-particle orbitals, subject to the constraint that the
orbitals are orthonormal and that the sum of the squares of the
orbitals give the exact ground state density.
.
They proposed focusing on the kinetic energy of a
non-interacting system of electrons as a functional of a set of
single-particle orbitals which give the exact density. Levy has
since presented a constrained search formulation of Kohn-Sham
theory in which the kinetic energy of a non-interacting system
of electrons is minimized with respect to a set of
single-particle orbitals, subject to the constraint that the
orbitals are orthonormal and that the sum of the squares of the
orbitals give the exact ground state density.
In the Kohn and Sham formulation of DFT, the kinetic
energy of a non-interacting system of electrons is minimized
with respect to a set of single-particle orbitals,{
 },
subject to the constraint that the orbitals are orthonormal and
that the sum of the squares of the orbitals gives the exact
ground state density. The Kohn-Sham variational principle is
},
subject to the constraint that the orbitals are orthonormal and
that the sum of the squares of the orbitals gives the exact
ground state density. The Kohn-Sham variational principle is
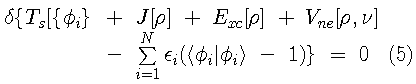
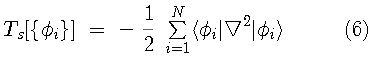
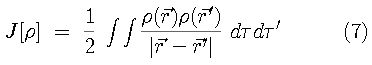
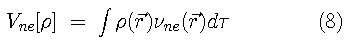
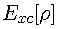 is the exchange-correlation energy (containing both kinetic and
potential contributions to the correlation energy), the
is the exchange-correlation energy (containing both kinetic and
potential contributions to the correlation energy), the
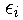 are Lagrange multipliers introduced to assure that
are Lagrange multipliers introduced to assure that
 are orthonormal and
are orthonormal and
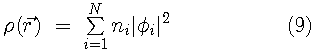
 .
.
The Kohn-Sham variational principle leads to a simple differential equation whose solutions are the Kohn-Sham orbitals,
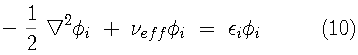
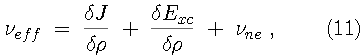
The Kohn-Sham Lagrange multipliers
![]() are not excitation energies as are the orbital energies of
Hartree-Fock theory. Instead, they reflect the response of the
total electronic energy to changes in occupation number, i.e.
are not excitation energies as are the orbital energies of
Hartree-Fock theory. Instead, they reflect the response of the
total electronic energy to changes in occupation number, i.e.

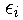 provide information about the electronegativity of the system.
Indeed, the electronegativity can be obtained from
provide information about the electronegativity of the system.
Indeed, the electronegativity can be obtained from
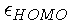 and
and
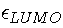 .
Although no Koopmans'-like theorem exists in Kohn-Sham theory,
excitation energies can be derived from the
.
Although no Koopmans'-like theorem exists in Kohn-Sham theory,
excitation energies can be derived from the
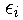 .
For instance, the first ionization energy can be found from
.
For instance, the first ionization energy can be found from
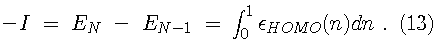
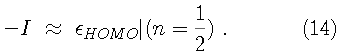
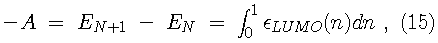
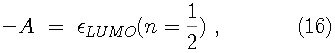
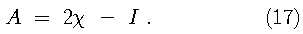
Since the Kohn-Sham orbitals give the total ground state electron density of the system, they also provide a practical method for calculating the local chemical reactivity properties discussed above. The Fukui reactivity indices may be obtained from the following equations:
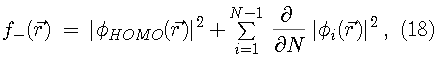
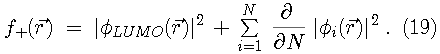
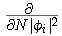 ,
can be ignored and the frontier molecular orbital theory as
first described by Fukui is recovered.
,
can be ignored and the frontier molecular orbital theory as
first described by Fukui is recovered.
Although the Kohn-Sham formalism is, in principle, exact, its
application is made inexact since the exchange-correlation
energy density functional,
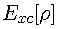 ,
is not known. Fortunately, reasonable approximations to
,
is not known. Fortunately, reasonable approximations to
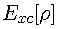 are known. The simplest approximation, due to Dirac and later
parameterized by Slater, works surprisingly well. More
elaborate approximations to
are known. The simplest approximation, due to Dirac and later
parameterized by Slater, works surprisingly well. More
elaborate approximations to
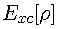 have been proposed and have proven useful in the calculation of
molecular properties. For many applications, local
approximations to
have been proposed and have proven useful in the calculation of
molecular properties. For many applications, local
approximations to
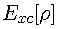 suffice. But, for those situations in which elongated bonds
(transition states, hydrogen bonds, etc) are involved,
non-local (gradient) corrections must be utilized. The
consequence of using an approximation to
suffice. But, for those situations in which elongated bonds
(transition states, hydrogen bonds, etc) are involved,
non-local (gradient) corrections must be utilized. The
consequence of using an approximation to
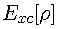 makes Kohn-Sham theory non-variational with respect to the exact
ground state energy. However, Kohn-Sham theory is variational
with respect to the model system described by the approximate
makes Kohn-Sham theory non-variational with respect to the exact
ground state energy. However, Kohn-Sham theory is variational
with respect to the model system described by the approximate
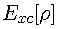 .
.
 Author: Ken Flurchick
Author: Ken Flurchick