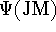 from configuration state functions (CSF),
from configuration state functions (CSF),
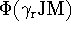 we proceed as follows,
we proceed as follows,
To build a multi-configuration atomic state function (ASF) denoted by
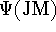 from configuration state functions (CSF),
from configuration state functions (CSF),
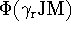 we proceed as follows,
we proceed as follows,
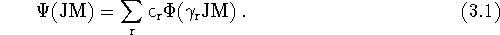
where the
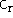 are the configuration mixing coefficients. Using this, the expectation
energy is written as,
are the configuration mixing coefficients. Using this, the expectation
energy is written as,
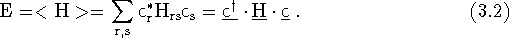
and the Hamiltonian matrix elements are,
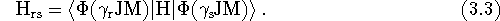
To prove this, note the expectation energy can be written as,
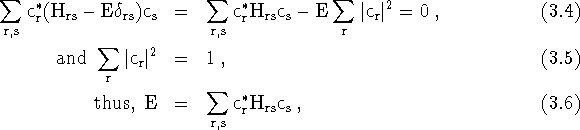
where
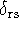 is the identity matrix.
is the identity matrix.
To evaluate the Hamiltonian matrix elements, the diagonal terms are,
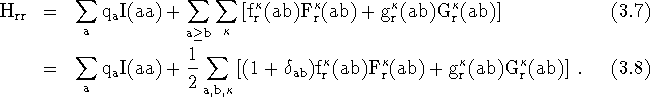
Note, all f,g,F and G functions are symmetric with respect to
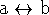 interchange. Also
interchange. Also
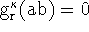 .
The off-diagonal terms are,
.
The off-diagonal terms are,
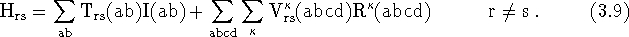
Now, the one particle radial integrals are,
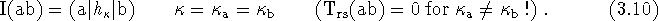
The two particle radial integrals are,
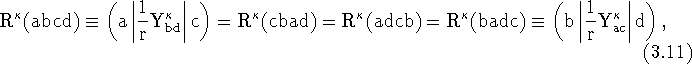
these are also known as Slater integrals. Also,
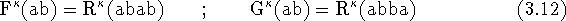
Y is Hartree's Y function given by,
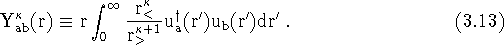
Now, perform a variation with respect to the mixing coefficients. In the multi-configuration scheme, the normalization condition becomes,
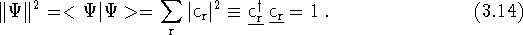
if
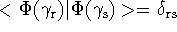 Then the variation wrt the mixing coefficients can be written as,
Then the variation wrt the mixing coefficients can be written as,
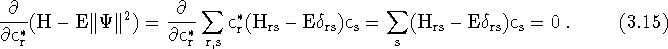
This leads to the matrix eigenvalue problem for the mixing coefficents,

Variation with respect to orbital a gives four different terms;
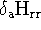 ,
,
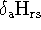 ,
,
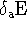 and
and
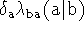 .
.
First, some definitions,
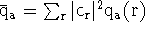 ,
,
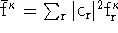 and,
and,
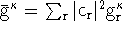 ,
,
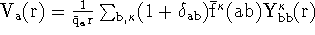 ,
,
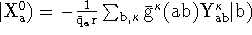 ,
,
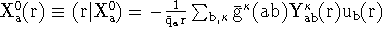 ,
,
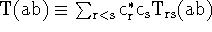 ,
,
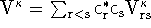 .
.
Using these definitions, the
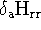 can be expressed as,
can be expressed as,
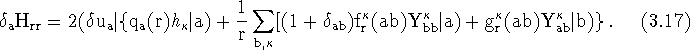
Then,
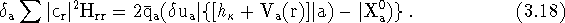
The
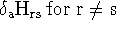 ,
similar to
,
similar to
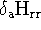 can be expressed as,
can be expressed as,
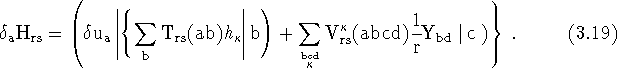
Then,
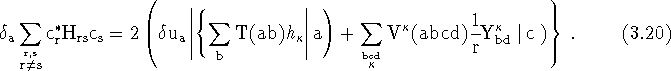
Next, the
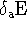 ,
,
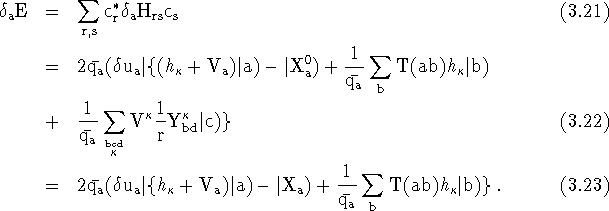
Where,
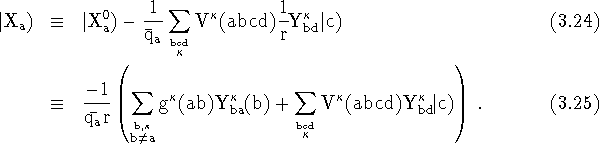
Note,

Finally, the Lagrange multiplier term,
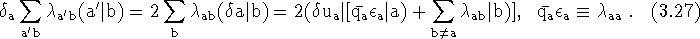
Finally, we obtain a multi-configuration Dirac-Fock orbital equation,
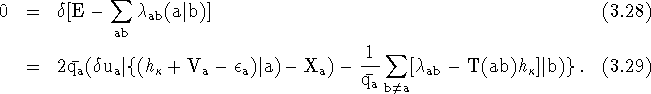
Therefore, the multiconfiguration orbital equations are,
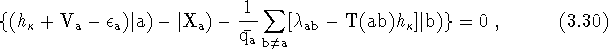
where,
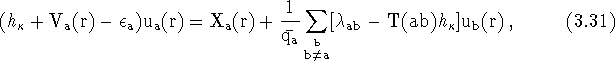
where,
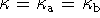 ,
and
,
and
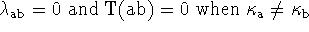 .
.
 Author: Dr. Warren Perger and Ken Flurchick
Author: Dr. Warren Perger and Ken Flurchick