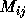Many chemistry problems are formulated in terms of states of a
chemical system, which can be labelled by an index corresponding to
species, choice of wave function, or internal excitation (see
Chapter 8 of [Fox:94a]). The calculation of energy levels,
potential or transition probability can often be related to a matrix
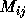whose rows and columns are just the possible system states.
M is often an approximation to the Hamiltonian of the system or it
could represent overlap between the states. There are two key stages
in such problems
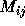
This structure has been elegantly exploited within the ``Global Array'' programming model built at Pacific Northwest Laboratory [Nicplocha:94a] with a set of tools (libraries) designed for this class of computational chemistry problem.
These two steps have very different characteristics. The matrix
element computations a), is of the embarrassingly parallel case as
each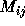 
can essentially be calculated independently even though
subexpressions may be shared between two or more distinct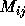 
.
Each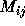 
is a multi-dimensional integral with the computation
depending on the details of the states i and j. Thus, this
computation is very time consuming and is not suited for SIMD
machines. The natural parallel algorithm associates sets of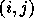 
with each node of a parallel computer. There are some relatively
straightforward load balancing issues and essentially no internode
communication. Thus, a MIMD cluster of workstations with modest
networking is sufficient for this step a). The final matrix
manipulations have quite a different character. These synchronous
problem components are suitable for SIMD machine and often required
substantial communication so that a workstation cluster will not be
effective. Matrix multiplication could be exception as it is
insensitive to latency and communication bandwidth for large matrices
and so suitable for workstation clusters.
One of the standard approaches to computational electromagnetics (CEM) is the method of moments [Harrington:61a;67a;68a], [Jordon:69a].
This is a spectral method, which rather than solving the underlying partial differential equation (Maxwell's), expands the desired solution in a set of ``moments''. This leads to a similar situation to that described above for computational chemistry where i and j label moments for CEM and not the chemical state [Cheng:94a;94c]. Note that in both cases, the matrix M is treated as full [Cheng:94c], and is quite different from the familiar sparse matrices gotten from discretizing a partial differential equation. We note in passing that such spatial discretization is a quite viable approach to CEM and leads to a totally different computational problem architecture from the spectral moment formulation.
HPF can handle both stages of the matrix based CEM or chemistry problems [Robinson:95a]. The matrix solution stage exploits fully the Fortran 90 array manipulation and clearly requires good compiler support for matrix and vector manipulation primitives. NPAC's experience with a production CEM code PARAMOM from the Syracuse Research Corporation is illuminating [Cheng:94c]. Both stages could be implemented on IBM SP-2 with specialized Fortran code for the matrix element generation joined to SCALAPACK based matrix solution [Choi:92c]. However, the CM-5 implementation was not so simple. The CMSSL library provided exceptional matrix solution with good use being made of the CM-5's vector nodes. However, the matrix element computation was not so straightforward. Performance on the CM-5 nodes was poor and required conversion of the original Fortran 77 to Fortran 90 to both exploit the vector nodes and link to CMSSL. However, whereas the Fortran 90 notation was very suitable for matrix manipulation, it is quite irrelevant for the matrix element generation stage---as already explained, this exploits the INDEPENDENT DO and not the array notation for explicit parallelism. Thus, we split the PARAMOM code into a metaproblem with two sub-problems corresponding to the two stages discussed above. Now we implemented each stage on the most appropriate architecture. The ``embarrassingly parallel'' Fortran 77 matrix element generation stage was run on a network of workstations, the equation solution stage used the optimized libraries on the CM-5 or SP-2. The linkage of these stages used AVS, but one could alternatively use many other coordination software approaches. We expect to test our use of World Wide Web technology WebWork [Fox:95a] on this example.
This simple example illustrates three problem classes: embarrassingly parallel, synchronous and metaproblems, and associated machine and software architecture. There is an interesting software engineering issue. Typically, one would develop a single Fortran program for such a computational chemistry or electromagnetics problem. However, better is separate modules---in this case, one for each of two stages---for each part of problem needing different parallel computer treatment. In this way, we see the breakup of metaproblems into components, and use of systems such as AVS as helpful software engineering strategies [Cheng:92a;94d]. We have successfully used such an approach to produce an effective parallel version of the public domain molecular orbital chemistry code MOPAC [MOPAC:95a].
Not all chemistry computations have this structure. For instance,
there is a set of applications such as AMBER and CHARMM that are based
on molecular dynamics simulations, as described in Chapter 16 of
[Fox:94a], [Ranka:92a]. These are typically loosely
synchronous problems with each particle linked to a dynamic set of
``nearest neighbors'' combined with long-range nonbonded force
computations. The latter can either use the synchronous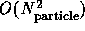 
algorithm or the faster, but complex loosely synchronous
fast multiple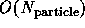 
or 
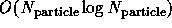approaches [Barnes:86a], [Edelsohn:91b],
[Goil:94a], [Goil:95a], [Greengard:87b],
[Salmon:90a], [Singh:93a], [Sunderam:93a],
[Warren:92b], [Warren:93a].