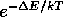Recall that a Monte Carlo algorithm will work only if it is ergodic, that is, it is possible to reach any state from any other state in a finite number of iterations.
The Metropolis algorithm is ergodic for T>0 since there is always a finite
probability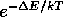 
of flipping a spin.
However, the algorithm may not be ergodic at T=0, since moving from one
ground state to another in a frustrated spin model may require higher energy
intermediate states.
For T very small, the probability of climbing out of a local minimum is non-zero, but may be so small that in any real simulation it will never happen. The system is then only quasi-ergodic.