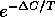 , where
, where 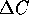 is the
change in the cost function due to a change in the configuration.
is the
change in the cost function due to a change in the configuration.
For a general optimization problem, the temperature is just a parameter that
governs the probability of increasing the cost function at any step, via the
usual Metropolis algorithm form 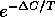 , where
, where 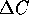 is the
change in the cost function due to a change in the configuration.
is the
change in the cost function due to a change in the configuration.
Just as for the spin glass, having a non-zero temperature allows the procedure to jump out of local minima. Zero temperature corresponds to a steepest descent type algorithm, where only changes that do not increase the energy are accepted.
Simulated annealing works well for many combinatorial optimization problems.