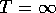 , with the susceptibility
, with the susceptibility 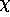 staying finite.
staying finite.
This model was proposed by Lenz in 1923 as a problem for his graduate
student, Ising, who showed that the 1-d model had no phase transition,
i.e. the magnetization varied continuously and slowly from T=0 to
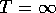 , with the susceptibility
, with the susceptibility 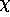 staying finite.
staying finite.
Onsager solved the 2-d problem exactly in 1944, showing that it had a phase transition of the type seen in real ferromagnets. This led to great advances in the theory of phase transitions and critical phenomena.
The 3-d problem also has a phase transition, but is not exactly soluble. Results come from analytic approximations and Monte Carlo simulation, which is the usual case for more complicated spin models.