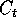 by the
introduction of a fictitious dynamics. The ``time'' t is computer time
(marking the number of iterations of the procedure), NOT real time --
our statistical system is considered to be in equilibrium, and thus
time invariant.
by the
introduction of a fictitious dynamics. The ``time'' t is computer time
(marking the number of iterations of the procedure), NOT real time --
our statistical system is considered to be in equilibrium, and thus
time invariant.
Let us set up a so-called Markov chain of configurations 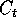 by the
introduction of a fictitious dynamics. The ``time'' t is computer time
(marking the number of iterations of the procedure), NOT real time --
our statistical system is considered to be in equilibrium, and thus
time invariant.
by the
introduction of a fictitious dynamics. The ``time'' t is computer time
(marking the number of iterations of the procedure), NOT real time --
our statistical system is considered to be in equilibrium, and thus
time invariant.
Let 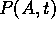 be the probability of being in configuration A at time t.
be the probability of being in configuration A at time t.
Let 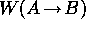 be the probability per unit time, or
transition probability, of going from A to B. Then:
be the probability per unit time, or
transition probability, of going from A to B. Then:
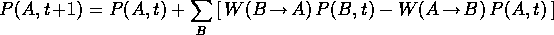
At large t, once the arbitrary initial configuration is ``forgotten,''
want 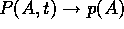 .
.