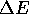 will be
large, so the probability to accept the change,
will be
large, so the probability to accept the change, 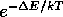 , will be
small. So update a single spin at a time.
, will be
small. So update a single spin at a time.
For the Ising model, the obvious change in the configuration is to try to
update (or ``flip'') a spin, i.e. flip the sign (or direction) of the spin
variable. If we try to change many spins at once, 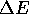 will be
large, so the probability to accept the change,
will be
large, so the probability to accept the change, 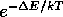 , will be
small. So update a single spin at a time.
, will be
small. So update a single spin at a time.
For a single spin flip, 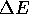 depends only on the spin values at the
site and its nearest neighbors, i.e. the update is local.
depends only on the spin values at the
site and its nearest neighbors, i.e. the update is local.
If 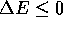 , we make the proposed change.
, we make the proposed change.
If 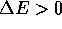 , we make the change with probability
, we make the change with probability 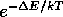 .
.