N.B. These are asymptotic
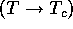 results.
results.
Second order transitions are classified by their critical exponents,
which measure how quantities diverge at the critical point.
N.B. These are asymptotic 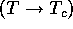 results.
results.
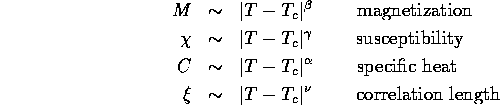
In many cases, these exponents (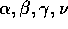 )
are universal, i.e., they do
not depend on details of the model, but only on gross features such as the
dimension of the space and the symmetries of the energy function.
This explains the success of very simple spin models like the Ising model in
providing a quantitative description of real magnets with complex interactions.
)
are universal, i.e., they do
not depend on details of the model, but only on gross features such as the
dimension of the space and the symmetries of the energy function.
This explains the success of very simple spin models like the Ising model in
providing a quantitative description of real magnets with complex interactions.