 goes like
goes like 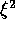 .
At the critical point,
.
At the critical point, 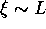 , so we expect
, so we expect 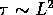 .
This is a major problem for MC simulations, since we need large L.
.
This is a major problem for MC simulations, since we need large L.
To decorrelate a configuration, need to make changes on a scale >
spatial correlation length. For local MC
algorithms (such as Metropolis) the effect of a change is only seen by nearest
neighbors. Since the update is a stochastic process, the changes should
propagate through the system like a random walk, so the number
of iterations required to propagate a distance  goes like
goes like 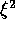 .
At the critical point,
.
At the critical point, 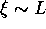 , so we expect
, so we expect 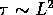 .
This is a major problem for MC simulations, since we need large L.
.
This is a major problem for MC simulations, since we need large L.
More generally, 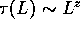 where z is called the dynamic
critical exponent.
For a local algorithm
where z is called the dynamic
critical exponent.
For a local algorithm 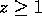 and usually
and usually 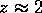 .
One of the active areas of research in MC simulation is
trying to find new algorithms with z<2.
These are usually non-local, multi-scale algorithms,
c.f. multigrid methods for solving PDEs,
where the same type of problem occurs.
.
One of the active areas of research in MC simulation is
trying to find new algorithms with z<2.
These are usually non-local, multi-scale algorithms,
c.f. multigrid methods for solving PDEs,
where the same type of problem occurs.