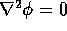 .
This can be discretized onto a 2-d grid, with the update depending only
on nearest neighbor points, e.g., an iterative scheme to solve this equation
would replace
.
This can be discretized onto a 2-d grid, with the update depending only
on nearest neighbor points, e.g., an iterative scheme to solve this equation
would replace 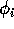 by the average value of its four neighbors.
by the average value of its four neighbors.
The Metropolis algorithm for a 2-d spin model is similar in many ways
to numerical methods for solving differential equations,
such as Laplace's equation 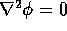 .
This can be discretized onto a 2-d grid, with the update depending only
on nearest neighbor points, e.g., an iterative scheme to solve this equation
would replace
.
This can be discretized onto a 2-d grid, with the update depending only
on nearest neighbor points, e.g., an iterative scheme to solve this equation
would replace 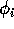 by the average value of its four neighbors.
by the average value of its four neighbors.
It is possible to iteratively update all sites at once (Jacobi algorithm). However, using a red/black update gives better convergence (like Gauss-Seidel). This is parallelized just like coarse grain parallel Metropolis algorithm.