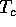Notice that this algorithm is purely SIMD, since every processor
does the same thing
at the same time. Since it propagates the label only one lattice spacing at a
step, the number of steps required to label the clusters is the maximum path
length (along bonded sites) between any two sites in the same cluster. For
cluster algorithms this will be order L (the length of the lattice), since
at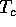 
there is one large cluster.
This method will work better for labeling small connected components, and worse for labeling objects such as spirals. The method is much too inefficient for cluster algorithms, basically because the parallel algorithm suffers from the same kind of ``critical slowing down'' (trying to label a large cluster using local steps) as does the sequential Metropolis algorithm!
Need a non-local parallel algorithm.