Computational Science and Information Technology meets GEM

1: Introduction

1.1: Computational Overview

The importance of simulating earthquakes is intuitively obvious. For instance, the recent January 16, 1995 Kobe, Japan earthquake was only a magnitude 6.9 event and yet produced an estimated $200 billion loss. Despite an active earthquake prediction program in Japan, this event was a complete surprise. Similar and more drastic scenarios are possible and indeed eventually likely in Los Angeles, San Francisco, Seattle, and other urban centers around the Pacific plate boundary. Earthquake simulations can help predict the level of shaking from a hypothetical event, and can help focus attention on areas and phenomena that need additional measurements or theoretical development.

There is substantial International interest in the use of large-scale computation in the earthquake field including an activity in Japan where major computational resources are being deployed and an effort among several Asia-Pacific nations including USA (the so-called APEC initiative). Here we will focus on an American activity known as GEM for its goal to produce a "General Earthquake Model" [gemhome].

There are currently no approaches to earthquake forecasting, which are uniformly reliable. The field uses phenomenological approaches, which attempt to forecast individual events or more reliably statistical analyses giving probabilistic predictions. The development of these methods has been complicated by the fact that large events responsible for the greatest damage repeat at irregular intervals of hundreds to thousands of years, and so the limited historical record has frustrated phenomenological studies. Direct numerical simulation has not been extensively pursued due to the complexity of the problem and the (presumed) sensitivity of the occurrence of large events to detailed understanding of both earth constituent make up and the relevant micro-scale physics which determines the underlying friction laws. However recently good progress has been made with a variety of numerical simulations and further both earth and satellite sensors are providing an increasing volume of data, which can be used to constrain and test the numerical simulations. This field is different from many other physical sciences such as climate and weather, as it so far has made little use of parallel computing and only now is starting its own "Grand Challenges". It is thus not known how important large-scale simulations will be in Earthquake science. Maybe simulations will never be able to predict the "big one" on the San Andreas fault but nevertheless it is essentially certain that they can provide a numerical laboratory of "semi-realistic" earthquakes with which other more phenomenological methods based on pattern recognition, can be developed and tested. As one can use data assimilation techniques to integrate real-time measurements into the simulations, simulations provide a powerful way of integrating data into statistical and other such forecasting methods.

This field has some individually very hard simulations but it has only just started to use high performance computers. Thus the most promising computations at this stage involve either scaling up existing simulations to large system sizes with modern algorithms or to integrate several component computations with assimilated data to provide early full fault system simulations. The latter has important real-world applications in the area of responding to and planning for crises as one can carry the computations through from initial sensing of stress build up through the structural simulation of building and civil infrastructure responding to propagating waves. This is discussed briefly in sections 5.3 and 5.4.

This field shows many different types of codes discussed in section 3, which eventually could be linked together to support either real time response to a crisis or fundamental scientific studies. The computational framework GEMCI introduced in section 2 has been carefully designed to support multiple types of linkage in terms of so-called problem solving environments.

1.2: Geoscience Overview

Earthquake science embodies a richness present in many physical sciences as there are effects present spread over more than ten orders of magnitude in spatial and temporal scales. (See figure 1 below).

Figure 1: Spatial and Temporal Scales in Earthquake Science

Success requires linking numerical expertise with the physical insight needed to coarse grain or average the science at a fine scale to be used phenomenologically in simulations at a given resolution of relevance to the questions to be addressed. Again the nonlinear fault systems exhibit a wealth of emergent, dynamical phenomena over a large range of spatial and temporal scales, including space-time clustering of events, self-organization and scaling. An earthquake is itself a clustering of slipped fault segments as seen in studies of critical phenomena. As in the latter field, one finds (empirically) scaling laws that include the well-known Gutenberg-Richter magnitude-frequency relation, and the Omori law for aftershocks (and foreshocks). Some of the spatial scales for physical fault geometries include:

The microscopic scale (~ 10-6 m to 10-1 m) associated with static and dynamic friction (the primary nonlinearities associated with the earthquake process).

The fault-zone scale (~ 10-1 m to 102 m) that features complex structures containing multiple fractures and crushed rock.

The fault-system scale (102 m to 104 m), in which faults are seen to be neither straight nor simply connected, but in which bends, offsetting jogs and sub-parallel strands are common and known to have important mechanical consequences during fault slip.

The regional fault-network scale (104 m to 105 m), where seismicity on an individual fault cannot be understood in isolation from the seismicity on the entire regional network of surrounding faults. Here concepts such as "correlation length" and "critical state" borrowed from statistical physics have led to new approaches to understanding regional seismicity.

The tectonic plate-boundary scale (105 m to 107 m), at which Planetary Scale boundaries between plates can be approximated as thin shear zones and the motion is uniform at long time scales.

2: GEM Computational Infrastructure (GEMCI)

2.1: Introduction

The components of GEMCI can be divided into eight areas.

1. Overall Framework including agreement to use appropriate "commodity industry standards" such as XML and CORBA, as well as more specialized high performance computing standards like MPI (Message Passing Interface).
2. Use of GEMCI to construct multiple Problem Solving Environments(PSE’s) to address different scenarios.
3. Web-based User Interface to each PSE
4. Simulation engines built in terms of the GEMCI framework
5. Geophysical specific libraries such as modules to estimate local physics and friction. These would also use the GEMCI framework which would already include generic libraries
6. Data analysis and Visualization
7. Data Storage, indexing and access for experimental and computational information
8. Complex Systems and Pattern Dynamics Interactive Rapid Prototyping Environment (RPE) for developing new phenomenological models -- RPE includes analysis and visualization aspects and would be largely on the client. In contrast, the large simulations in 4) above, are naturally thought of as distributed server side computational objects.

In the remainder of this section, we describe the overall GEMCI framework and how it can be constructed in terms of components built according from emerging distributed object and Web standards and technologies. This describes the "coarse grain" (program level) structure of the GEMCI environment. There are myriad important details inside each module, which could be a finite element simulation code, data streaming from a sensor, a visualization subsystem, a Java eigensolver used in the client RPE or field data archived in a web-linked database. In section 3, we describe some of the existing simulation modules available to the GEM collaboration while section 4 goes into one case in detail. This is the use of fast multipole methods in large-scale Green’s function computations. Section 5 illustrates how these ideas can be integrated together into a variety of different scenarios. These essentially correspond to different problem solving environments that can be built by using the same GEMCI framework to link GEM components in various ways. In section 6, we make brief remarks on other parts of the GEMCI framework and speculate a little on the future. There are several important activities which have pioneered the use of object based techniques in computational science. Legion has developed a sophisticated object model optimized for computing [legion] and such a framework could be integrated into GEMCI. Currently we are focussing on broad capabilities available in all important distributed object approaches and we can refine this later as we develop more infrastructure. Nile developed the use of CORBA for experimental data analysis [nile] but we need a broader functionality. POOMA is an interesting technology developed at Los Alamos [pooma] aimed at object oriented methods for finer grain objects used to build libraries as discussed in section 2.5. GEMCI could use modules produced by POOMA as part of its repository of coarse grain distributed components.

2.2: Distributed Objects and the Web

2.2.1: Multi-Tier Architectures

Fig 2: 3-Tier Computing Model illustrated by Basic Web Access

Modern information systems are built with a multi-tier architecture that generalizes the traditional client-server to become a client-broker-service model. This is seen in its simplest realization with the classic web access which involves 3 tiers – the Browser runs on a client; the middle-tier is a Web server; the final tier or backend is the file system containing the Web page. One could combine the Web server and file system into a single entity and return to the client-server model. However the 3-tier view is better as it also captures the increasingly common cases where the Web Server does not access a file system but rather the Web Page is generated dynamically from a backend database or from a computer program invoked by a CGI script. More generally the middle tier can act as an intermediary or broker that allows many clients to share and chose between many different backend resources. This is illustrated in Fig. 3, which shows this architecture with the two interfaces separating the layers. As we will discuss later the specific needs and resources of the Earthquake community will be expressed by metadata at these interfaces using the new XML technology.

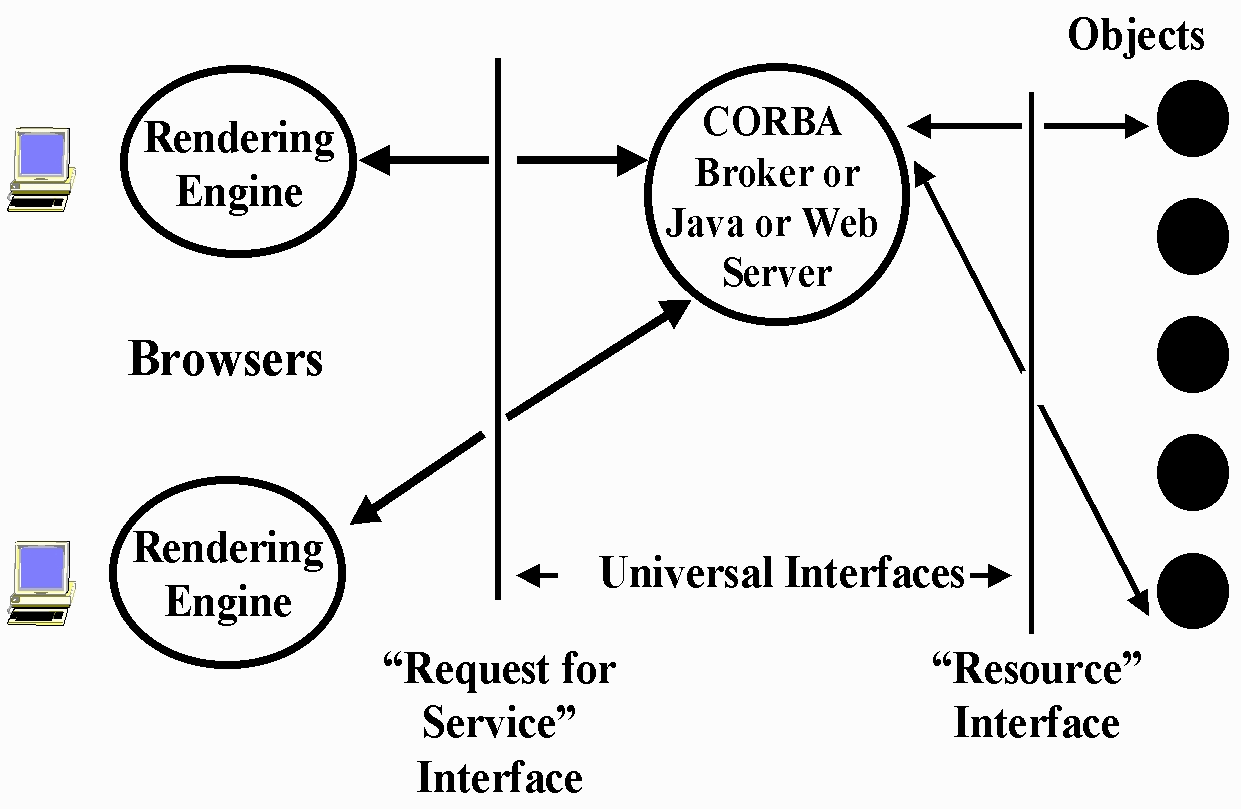
Fig 3: General Three Tier Architecture

This 3-tier architecture (often generalized to a multi-tier system with several server layers) captures several information systems which generalize the access to a web page in Fig. 2 and the invocation of a computer program from a Web or other client in Fig 4.

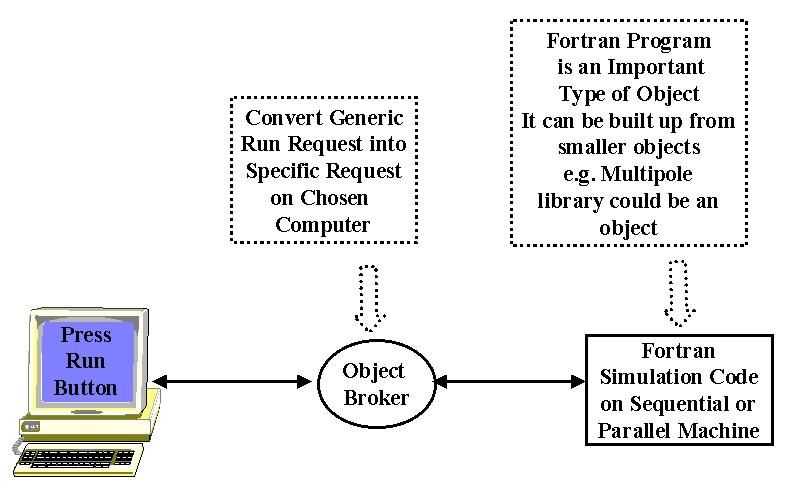
Fig 4: Simple Simulation formulated as a "distributed computational object"

The architecture builds on modern distributed object technology and this approach underlies the "Object Web" approach to building distributed systems. Before describing this, let us define and discuss several computing concepts.

2.2.2: Clients, Servers and Objects

A server is a free standing computer program that is typically multi-user and in its most simplistic definition, accepts one or more inputs and produces one or more outputs. This capability could be implemented completely by software on the server machine or require access to one or more (super)computers, databases or other information resources such (seismic) instruments. A client is typically single-user and provides the interface for user input and output. In a distributed system, multiple servers and clients, which are in general geographically distributed, are linked together. The clients and servers communicate with messages for which there are several different standard formats. An (electronic) object is essentially any artifact in our computer system. As shown in Fig. 4, a computer program is one form of object while the best known distributed object is a web page.

In the example of fig. 2, a Web Server accepts HTTP request and returns a web page. HTTP is a simple but universal protocol (i.e. format for control information) for messages specifying how Web Clients can access a particular distributed object – the web page. Again a Database Server accepts a SQL request and returns records selected from database. SQL defines a particular "Request for Service" in the interface of fig. 3 but usually the messages containing these requests use a proprietary format. New standards such as JDBC (The Java Database Connectivity) imply a universal message format for database access with vendor dependent bridges converting between universal and proprietary formats. An Object Broker as in fig. 4 uses the Industry CORBA standard IIOP message protocol to control the invocation of methods of a distributed object (e.g. run a program). IIOP and HTTP are two standard but different protocols for communicating between distributed objects.

2.2.3: Services in a Distributed System

Distributed objects are the units of information in our architecture and we need to provide certain critical operating system services to support them. Services include general capabilities such as "persistence" (store information unit as a disk file, in a database or otherwise), and "security" as well as more specialized capabilities for science such as visualization. One critical set of services is associated with the unique labeling of objects and their look-up. We are familiar with this with Domain Name Servers and Yellow Page services for computers on the Internet. Web pages with URL’s build on this technology and Web search engines like AltaVista provide a sophisticated look-up service. More general objects can use natural variants of this approach with a possibly arcane URL linking you to a database, supercomputer or similar resource. The "resource" interface in fig. 3 defines the properties of back-end resources and how to access them. In particular it defines the equivalent of a URL for each object. The set of these resource specifications forms a database, which defines a distributed object repository.

2.2.4: XML Extended Markup Language

The new XML technology is used to specify all resources in the GEMCI. A good overview of the use and importance of XML in Science can be found in [SciAm] and we illustrate it below in Fig. 5, which specifies a computer program used in a prototype GEM problem solving environment described later and shown in figs 15 and 16.

Fig. 5: XML Used to describe the computational problem defined in fig. 14

Readers who are familiar with HTML will recognize that XML has a similar syntax with elements defined by nested tags such as <application > …. </application>. This information is further refined by attribute specification as in the string id=disloc, which naturally indicates that this is the disloc application code. XML is a very intuitive way of specifying the structure of digital objects as simple ASCII byte streams. One could equally well specify the same information by appropriate tables in an object-relational database like Oracle, and indeed XML files can easily be stored in such a database if you require their powerful data access and management capabilities. Correspondingly relational database contents can easily be exported to XML format. XML is obviously more easily written and read than a complex database. Further there are growing set of powerful tools which can process XML – these include parsers, editors and the version 5 browsers from Microsoft and Netscape which can render XML under the control of a powerful language XSL which specifies the mapping of tags to the display device. In the multi-tier generalization of Fig. 3, one has multiple linked servers in the middle tier. These servers exchange information, which is expressed as a stream of objects. These objects need to be "serialized" so as to be transportable between servers. There are many ways of converting complex data-structures into a stream of bytes but XML is one of the most general and often the best choice.

2.2.5: Dynamic Resources

Traditionally one labels a computer with an IP address that reflects a particular physical domain or addresses a web page with a URL, which reflects a particular server and file system. This approach is appropriate for a fixed resource but not well designed for mobile or dynamic resources such as palm top devices and the growing number of Internet enabled consumer products. These resources are often transient and one cannot assume their continuous availability. There is substantial academic and commercial interest in new object registration, look-up and connection approaches supporting fault tolerance and dynamic clients and servers. Objects must be self defining and able to announce themselves universally to a network of registration servers. Jini from Sun Microsystems [jini] and the Ninja system from UC Berkeley [ninja] are well known examples of new approaches to dynamic objects.

2.2.6: The Object Web

The Object Web signifies the merger of distributed object and web technologies, which is implicitly embodied in the discussion above. There are four rather distinct but important

Object standards. CORBA is the Industry Standard supporting objects in any language on any platform. New features in CORBA tend to be deployed relatively slowly as they have a cumbersome approval process and must satisfy complex constraints. COM is the Microsoft standard, which is confined to PC’s but broadly deployed there and high performance. Java is the software infrastructure of the web and although single language, the same object can be used on any computer supporting the Java VM. XML comes from the Web Consortium and has been briefly described above. It can be used to define general objects in an intuitive format illustrated in fig. 5.

The Pragmatic Object Web implies that there is no outright winner in the distributed object field and one should mix and match approaches as needed. For instance, CORBA Objects can use interfaces (as in fig. 3) defined in XML, Clients and Servers programmed in Java, with rendered displays using COM.

2.3: Architecture of the GEMCI Problem Solving Environment

A Problem Solving Environment or PSE is an application that integrates access to the data, computers and tools needed for a particular computational science area. There is general agreement that Object Web technology is the natural software infrastructure for building PSE’s for the entities one needs to integrate can be considered as distributed objects. With this choice, there is a growing trend to term web-based PSE’s as portals in analogy to the term used to describe environments built commercially to allow access to personal or business information. Commercial portals allow both administrative and user customizability from a suite of objects and services supporting them.

GEMCI illustrated in fig. 6, is an Object Web PSE and has the classic 3 tier structure discussed above.

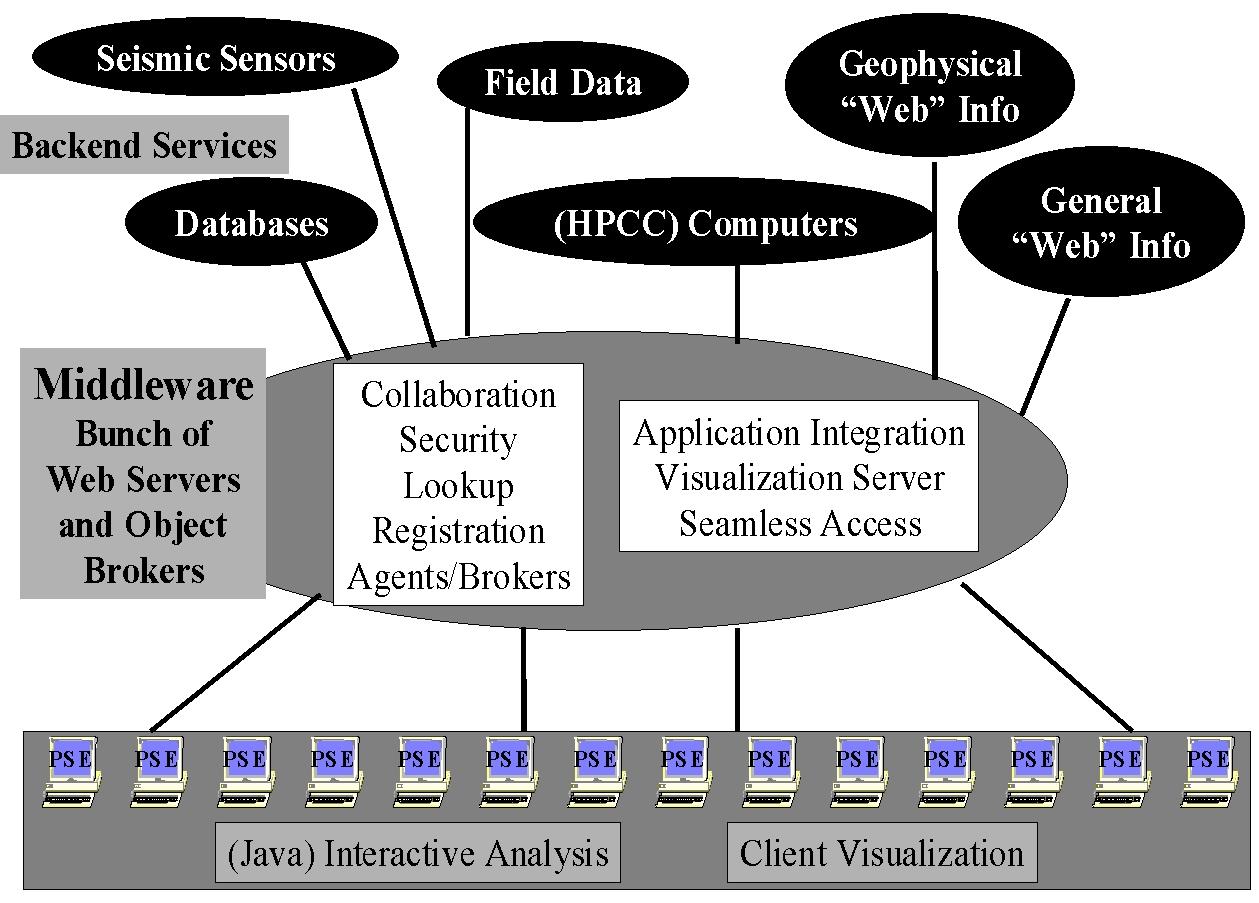
Fig. 6: 3 Tier Architecture of a GEM Problem Solving Environment

In GEMCI, everything is a "distributed object" whether it be a simulation on a supercomputer; the basic GEM Web pages; the notes from a field trip entered on a palm top; CNN real-time coverage of the latest earthquake or the data streaming in from sensors. GEMCI provides an integrated view of these diverse resources with XML definitions for the raw objects themselves and the data they produce. The services shown in fig 6, from collaboration, security, object discovery, visualization and computer access, are generic to all computing portals. Building GEMCI using the same approach and tools as other portals ensures the availability of these services. They will require customization as for instance there are many different visualization packages and each requires non trivial work to include in such a portal. Again collaboration corresponds to sharing distributed objects, and this can currently only be automated for some objects. Many web pages can be shared using generic techniques illustrated in fig. 5 but sharing say the control and output of a general simulation can require quite a lot of custom modifications.

Most importantly using GEMCI shown in fig. 6, one needs to define the entities in the GEM environment as distributed objects. For computer programs this implies a rather arcane process termed "wrapping the program as a distributed object". Operationally this implies allowing a middle-tier server (the CORBA object broker or Java application Server) to be able to run the program on one or more machines, specify the input files and either specify output files or access them as streams of data in fashion of UNIX pipes. Each distributed object technology has a rather different approach to this using what is termed an IDL or Interface Definition Language and specialized Java and C++ code to implement the wrapping. However, we can use the concept of the Pragmatic Object Web to simplify this process. Our strategy is to define all relevant properties of computer programs in XML as illustrated in fig. 5. These properties are used to generate either statically or dynamically the needed object wrappers. This approach requires the user specify what they know – the properties of their program, while the filter copes with the obscure syntax of each object model. Obviously this also allows one to support all object models – COM CORBA Java, by changing the filter and so one can adapt to changes in the commercial infrastructure used in the middle tier.

One must apply the XML object definition strategy to all entities in GEMCI; programs, instruments and other data sources and repositories. This gives the metadata defining macroscopically the object structure. However equally usefully, one needs to look at the data stored in, produced by or exchanged between these objects. This data is itself a typically a stream of objects – each an array, a table or more complex data structure. One could choose to treat the data at some level as an unspecified (binary) "blob" with XML defining the overall structure but detailed input and output filters used for the data blobs. As an example, consider the approach that an electronic news organization could take for their data. The text of news flashes would be defined in XML but the high volume multimedia data (JPEG images and MPEG movies) would be stored in binary fashion with XML used to specify <IMAGEOBJECT> or <MOVIEOBJECT> metadata. As explained earlier, systematic use of XML allows use of a growing number of tools to search, manipulate, store persistently and render the information. It facilitates the linkage of general and specific tools/data sources/programs with clearly defined interfaces. This will help the distributed GEM collaborators to separately develop programs or generate data, which will be easily able to interoperate. More generally XML standards will be defined hierarchically starting with distributed information systems, then general scientific computing and finally application specific object specifications. For example GEMCI would develop its own syntax for seismic data sensors but could build on general frameworks like the XSIL scientific data framework developed at Caltech [xsil]. XSIL supports natural scientific data structures like arrays and the necessary multi-level storage specification. Another example is MathML which provides XML support for the display and formulation of Mathematics. We can expect MathML to be supported by tools like Web Browsers and white boards in collaborative scientific notebooks and allow one to enhance theoretical collaboration in GEM. There will for instance be modules that can be inserted into applications for parsing MathML or providing graphical user specification of mathematical formulae. This could be used in sophisticated implementations of the Complex Systems and Pattern Dynamics Interactive Rapid Prototyping Environment with scripted client side specification of new analysis methods. One can also use MathML in high level tools allowing specification of basic differential equations that are translated into numerical code. This has been demonstrated in prototype problem solving environments like PDELab but have so far not had much practical application [pdelab]. Greater availability of standards like MathML should eventually allow more powerful interchangeable tools of this type. Finally we can mention a set of graphical XML standards such as X3D (3 dimensional objects) and VML which is a vector graphics standard, which can be expected to be important as basis of application specific plot and drawing systems.

2.4: Building the GEMCI Problem Solving Environment

We have described above some aspects of the base strategy of defining GEM components as distributed objects. Here we discuss some existing experience from NPAC at Syracuse in integrating such objects and tools that manipulate them into an overall environment. The NPAC team has built several exemplar problem solving environments for both the NSF and DoD HPCMO (High Performance Computing Modernization Office) supercomputer centers. In fig. 7, we show some useful tools including a first cut at a "wizard" that helps produce the distributed object wrappers described above.

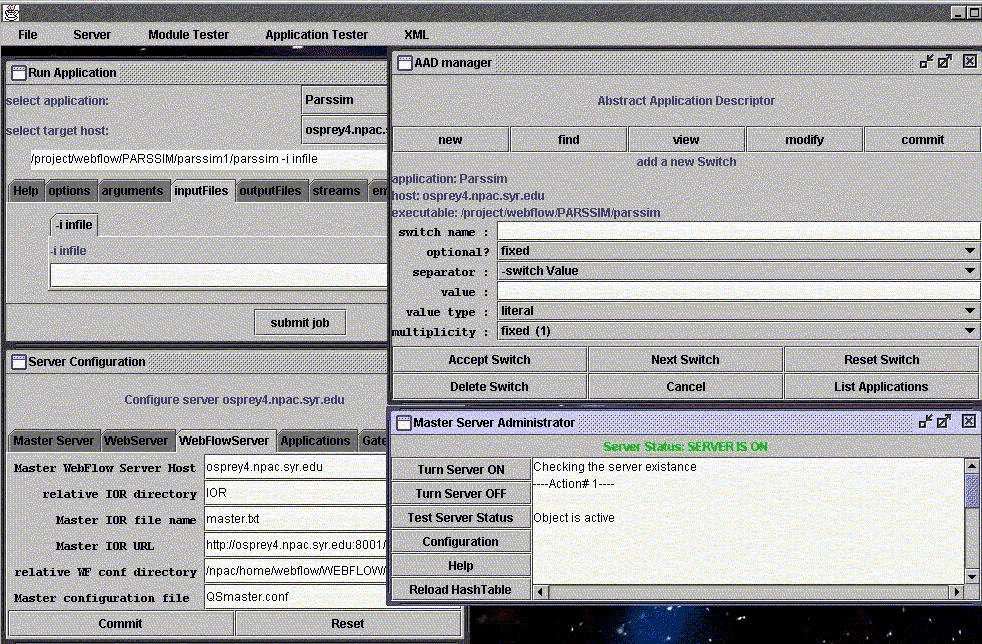
Fig. 7: This illustrates several components of the WebFlow system from NPAC. (Counter-clockwise from bottom-left): The Server Configuration and Master Server Administrator are WebFlow administrative tools that allow one to configure and monitor the middle tier servers. AAD manager (Abstract Application Descriptor) is a tool to incorporate new applications to the system: the interface shown simplifies creation of an XML definition of the application.

This definition can be used for dynamical creation of front-end application interfaces (window "Run Application").

This AAD (Abstract Application Descriptor) can be extended to allow specification of all needed input parameters of an application, with an automatic generation of input forms respecting default values and allowed value ranges. The object wrappers of an application should not only invoke the code and allow parameter specification but have built in description/help systems.

One major NPAC Problem Solving Environment was built for the Landscape Management System (LMS) project at the U.S. Army Corps of Engineers Waterways Experiment Station (ERDC) Major Shared Resource Center (MSRC) at Vicksburg, MS, under the DoD HPC Modernization Program, Programming Environment and Training (PET). The application can be idealized as follows.

A decision maker (the end user of the system) wants to evaluate changes in vegetation in some geographical region over a long time period caused by some short term disturbances such as a fire or human’s activities. One of the critical parameters of the vegetation model is soil condition at the time of the disturbance. This in turn is dominated by rainfall that possibly occurs at that time. Consequently as shown in fig. 8, the implementation of this project requires:

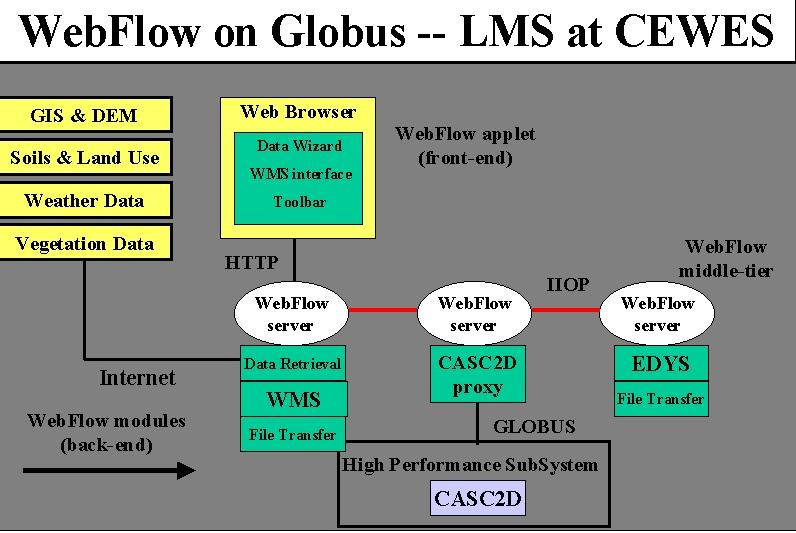
Fig. 8: 3 Tier Architecture of DoD "Land Management" Application whose front end is shown in fig. 9

• Data retrieval from remote sources including DEM (data elevation models) data, land use maps, soil textures, dominating flora species, and their growing characteristics, to name a few. The data are available from many different sources, for example from public services such as USGS web servers, or from proprietary databases. The data come in different formats, and with different spatial resolutions.

• Data preprocessing to prune and convert the raw data to a format expected by the simulation software. This preprocessing is performed interactively using WMS (Watershed Modeling System) package.

• Execution of two simulation programs: EDYS for vegetation simulation including the disturbances and CASC2D for watershed simulations during rainfalls. The latter results in generating maps of the soil condition after the rainfall. The initial conditions for CASC2D are set by EDYS just before the rainfall event, and the output of CASC2D after the event is used to update parameters of EDYS and the data transfer between the two codes had to be performed several times during one simulation. EDYS is not CPU demanding, and it is implemented only for Windows95/98/NT systems. On the other hand, CASC2D is very computationally intensive and typically is run on powerful backend supercomputer systems.

• Visualization of the results of the simulation. Again, WMS is used for this purpose.

One requirement of this project was to demonstrate the feasibility of implementing a system that would allow launching and controlling the complete simulation from a networked laptop. We successfully implemented it using WebFlow middle-tier servers with WMS and EDYS encapsulated as WebFlow modules running locally on the laptop and CASC2D executed by WebFlow on remote hosts. Further the applications involved showed a typical mix of supercomputer and computationally less demanding personal computer codes. LMS was originally built using specialized Java Servers but these are now being replaced by commercial CORBA object brokers but in either case the architecture of fig. 8 is consistent with the general structure of fig. 6 and 3.

For this project we developed a custom front-end shown in fig. 9, that allows the user to interactively select the region of interest by drawing a rectangle on a map. Then one could select the data type to be retrieved, launch WMS to preprocess the data and make visualizations, and finally launch the simulation with CASC2D running on a host of choice.

Fig 9: Example of a Web Interface for a "Land Management Problem Solving Environment" built by NPAC for the Department of Defense ERDC Laboratory in Vicksburg, Ms.

Our use of XML standards at the two interfaces in fig. 3, allows us to change front end and middle-tier independently. This allowed us the middle tier upgrade described above which will bring security and "seamless access" capability to our PSE’s.

Seamless access is an important service, which is aimed at allowing applications to be run on an arbitrary appropriate backend. Most users wish their job to just run and usually do not mind what machine is used. Such seamless capability is rather natural in the architecture of fig. 3. Essentially the front end defines the "abstract" job passing its XML specification to a middle tier server. This acts as a broker and instantiates the abstract job on one of the available backend computers. The middle-tier backend XML interface is used to specify both the available machines sent to the servers and the "instantiated job" sent from the servers. We build the back end mapping of jobs to machine using the important Globus technology [globus].

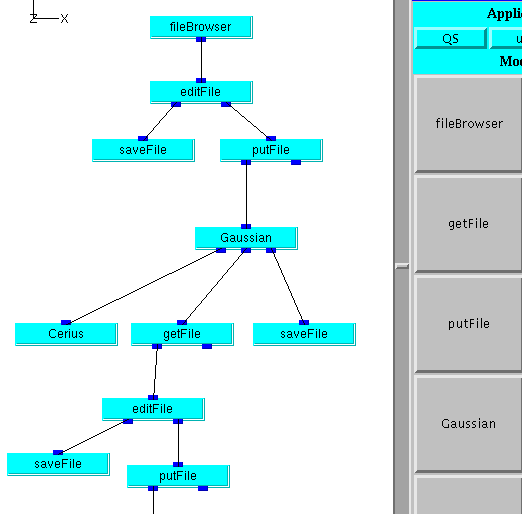
Fig 10: Fragment of WebFlow Composition Tool linking modules in a Quantum Simulation (Chemistry) application

One can view WebFlow as a "kit" of services, which can be used in different ways in different applications. In fig. 10, we show another capability of WebFlow, which supports the ability to compose complex problems by linking different applications together with data flowing between different modules chosen from a palette. This WebFlow service is supported by a Java front end and a middle tier service matching abstract modules to back end computers and supporting the piping of data between the modules.

2.5: Libraries or Distributed Components?

Since the beginning of (computing) time, large programs have been built from components that are assembled together into a complete job. One can do this in many ways and perhaps the best known is the use of libraries linked together. Modern "object-oriented" approaches can be used in this fashion with method calls. Design frameworks can be used to establish a systematic methodology with say specific interfaces ("calling sequences") to be followed by for instance different implementations of friction laws. The discussion in section 2.4 above describes a rather different component model where possibly distributed modules are linked together in a dynamic fashion. This is more flexible than library approach and further as explained above, this supports distributed components. The component approach is not surprisingly less efficient than the library approach as component linkage is typically obtained through explicit exchange of messages rather efficient compiled generated parameter passing as for methods. The inefficiency is particularly serious for small components as the component mechanisms come with large start up (latency) overheads. Thus we adopt a hybrid approach with small objects using the traditional library mechanism within a set of agreed interfaces and design frameworks to promote easier interchange of modules. Large objects (roughly "complete programs") use a component approach within a distributed object framework defined as we suggest in XML.

3: Current GEM Computational Components

The first step in building the GEMCI has been to inventory the computer codes currently available in the community. A summary of the results of this inventory is maintained at http://milhouse.jpl.nasa.gov/gem/gemcodes.html and the status as of the time of writing is given below.

The categories covered by the existing codes include codes for understanding dislocations: elastic models - both half-space and layered, viscoelastic models, finite element and boundary element codes, and inversion codes. There are a set of codes for understanding how faults interact: cellular automata, finite element and boundary element codes, fault friction models. Some codes are designed to understand the dynamics of the earthquake rupture itself. Finally there are codes for displaying the results of various simulations. We follow with short descriptions of the codes grouped by type.

Elastic

• 3D-DEF -- Performs elastic dislocation boundary-element calculations
• coulomb -- Computes 3D elastic dislocation & 2D boundary element stress and strain
• DYNELF -- Models 3D elastodynamic finite difference with frictional faults
• faultpatch -- Generates earthquake sequences, given fault geometries and loading rates using

Cellular automata methods

• FLTSLP -- Inverts groups of focal mechanism solutions or slickenline data for orientation and relative magnitudes of principal strain rates and for relative micropolar vorticity.
• GNStress -- Model stresses induced by faulting, for studying fault interaction.
• layer -- Calculates surface displacements and strains for vertical strike-slip point source in horizontal layer above half-space.
• RNGCHN -- Calculate surface displacements and strains in elastic half space.
• scoot -- 2D elastodynamic finite difference with frictional fault
• simplex -- 3D inversion of geodetic data for displacement on faults.

Viscoelastic

• DYNELF -- Models 3D elastodynamic finite difference with frictional faults
• FLTGRV and FLTGRH -- Compute 3 vector components of surface displacement from slip on a dipping thrust fault contained within an elastic layer overlying a viscoelastic-gravitational half space.
• STRGRH and STRGRV -- Computes 3 vector components of surface displacement from slip on a dipping strike slip fault contained within an elastic layer overlying a viscoelastic-gravitational half space.
• Virtual_California -- Realistic cellular automata (CA) viscoelastic earthquake simulator.
• VISCO1D -- Computes viscoelastic spherical deformation due to faulting or dike emplacement.

Cellular Automata

• faultpatch -- Generates earthquake sequences, given fault geometry’s and loading rates using Cellular automata methods.
• Virtual_California -- Realistic cellular automata (CA) viscoelastic earthquake simulator.

Dynamic

• DYNELF -- Models 3D elastodynamic finite difference with frictional faults
• scoot -- 2D elastodynamic finite difference with frictional fault

Inverse

• FLTSLP -- Inverts groups of focal mechanism solutions or slickenline data for orientation and relative magnitudes of principal strain rates and for relative micropolar vorticity.
• simplex -- 3D inversion of geodetic data for displacement on faults.
• qoca

Visualization

• VelMap -- Aid for visualizing displacement and velocity of crust.

4: Large-scale Simulations in GEMCI

4.1: Overview of Earthquake Fault System Simulations

With reasonable approximation, you can model the long-term evolution of stresses and strains on interacting fault segments with a Green's function approach. As in other fields this method leads to a boundary (the faults) value formulation, which looks numerically, like the long-range force problem. The faults are paneled with segments (with area of some 100 m² in definitive computations) which interact as though they were dipoles. The original calculations of this model used the basic O(N²) algorithm but a new set of codes will be using the "fast multipole" method. There are interesting differences between the earthquake and gravitational applications. In gravity we get wide ranges in density and dynamical effects from the natural clustering of the gravitating particles. Earthquake "particles" are essentially fixed on complex fault geometries and their interactions fall off faster than those in the astrophysical problem.

Several variants of this model have been explored including approximations, which only keep interactions between nearby fault segments. These "cellular automata" or "slider-block" models look very like statistical physics with an earthquake corresponding to clusters of particles slipping together when the correlation length gets long near a critical point. The full Green's function approach should parallelize straightforwardly in either O(N²) or multipole formulation. However cellular automata models will be harder to parallelize, as we know from experience with the corresponding statistical physics case where clustering models have been extensively studied.

An interesting aspect of these simulations is that they give the "numerical laboratory" for the study of space-time patterns in seismicity information. This type of analysis was used successfully in the climate field to aid the prediction of "El Nino" phenomena. These pattern analyses may or may not need large computational resources although they can involve determination of eigensolutions of large matrices which is potentially time consuming.

4.2: Green’s Function Formulation and Approximations

4.2.1: Basic Equations

Let us consider in more detail the problem addressed by the Virtual_California code described in section 3 and introduced in Rundle 1988a. If one is given a network of faults embedded in an Earth with a given rheology, subject to loading by distant stresses, and neglecting elastic waves (see discussion below), the evolution of the state of slip s(x,t) on a fault at (x,t) is determined from the equilibrium of stresses according to Newton's Laws:

¶s(x,t) / ¶t=F {S i (si) } (1)

where F{} is a nonlinear functional, and Si(si) represents the sum of all stresses acting within the system. These stresses include

• The interaction stress sint[x,t; s(x',t'); p] provided by transmission of stress through the Earth's crust arising from background tractions p, as well as stresses due to slip on other faults at other sites x' at times t';

• The cohesive fault frictional stress sf[x,t; s(x,t)] at the site (x,t) associated with the state of slip s(x,t); and

• Other stresses such as those due to dynamic stress transmission and inertia.

The transmission of stress through the Earth's crust involves both dynamic effects arising from the transient propagation of seismic waves, and from static effects that persist after wave motion has ceased. Rheologic models typically used for the Earth's crust between faults are all linear (e.g., Rundle and Turcotte, 1993) and include

• A purely elastic material on both long and short time scales;

• A material whose instantaneous response is elastic but whose long term deformation involves bulk flow (viscoelastic); and

• A material that is again elastic over short times, but whose long term response involves stress changes due to the flow of pore fluids through the rock matrix (poroelastic).

In fig. 11, we show the basic conceptual "wiring diagram" for the model, which indicates the interplay between loading stresses, rupture, interactions with other faults, and relaxation processes following a major earthquake.

4.2.2: The Green's Function Approximation

Considering GEM models that assume a linear interaction rheology between the faults implies that the interaction stress can be expressed as a spatial and temporal convolution of a stress Green's function Tijkl (x-x',t - t') with the slip deficit variable f(x,t)=s(x,t) - Vt, where V is the long term rate of offset on the fault. Once the slip deficit is known, the displacement Green's function Gijk(x-x',t-t') can be used to compute, again by convolution, the deformation anywhere in the surrounding medium exterior to the fault surfaces (e.g. Rundle 1988a). In the first implementation of GEM models, we expect to specialize in the case of quasistatic interactions, even during the slip events. Observational evidence supports the hypothesis that simulations carried out without including inertia and waves will have substantial physical meaning. Kanamori and Anderson (1975) and Kanamori et al. (1998) estimated that the seismic efficiency h, which measures the fraction of energy in the earthquake lost to seismic radiation, is less than 5%-10%, implying that inertial effects in the dynamical evolution of slip in studying large populations of earthquakes will be of lesser importance for initial calculations. Elastic waves will be included in later simulations when errors arising from other effects are reduced to the 5%-10% level. At present, inclusion of these effects is severely limited by available computational capability, so we anticipate that it may be only practical to include only the longest wavelengths or largest spatial scales.

4.2.3: Inelastic Rheologies:

In quasistatic interactions, the time dependence of the Green's function typically enters only implicitly through time dependence of the elastic moduli (e.g., Lee, 1955). Because of linearity, the fundamental problem is reduced to that of calculating the stress and deformation Green's function for the rheology of interest. For materials that are homogenous within horizontal layers, numerical methods to compute these Green's functions are well known (e.g., Okada, 1985, 1992; Rundle, 1982a,b, 1988; Rice and Cleary, 1976; Cleary, 1977; Burridge and Varga, 1979; Maruyama, 1994). Problems in heterogeneous media, especially media with a distribution of cracks too small and too numerous to model individually, are often solved by using effective medium approaches, self-consistency assumptions (Hill, 1965; Berryman and Milton, 1985; Ivins, 1995a,b), or damage models Lyakovsky et al. (1997). Suffice to say that a considerable amount of effort has gone into constructing quasistatic Green's functions for these types of media, and while the computational problems present certain challenges, the methods are straightforward as long as the problems are linear. In the initial work, we expect to focus on elastic (with possible incorporation of damage parameters) and layered viscoelastic models only.

4.3: Friction Models:

Friction models to determine the slip condition must augment the overall differential equations. At the present time, six basic classes of friction laws have been incorporated into computational models.

1. Two basic classes of friction models arise from laboratory experiments:

Slip Weakening This friction law (Rabinowicz, 1965; Bowdon and Tabor, 1950; Beeler et al., 1996; Stuart, 1988; Li, 1987; Rice, 1993; Stuart and Tullis, 1995) assumes that the frictional stress at a site on the fault sf=sf[s(x,t)] is a functional of the state of slip. In general, sf[s(x,t)] is peaked at regular intervals. The current state of the system is found from enforcing the equality sf[s(x,t)]=sint[x,t; s(x',t'); p] prior to, and just after, a sliding event.

Rate and State . These friction laws are based on laboratory sliding experiments in which two frictional surfaces are slid over each other at varying velocities, usually without experiencing arrest (Dieterich, 1972; 1978; 1981; Ruina, 1983; Rice and Ruina, 1983; Ben Zion and Rice, 1993; 1995; 1997; Rice, 1993; Rice and Ben Zion, 1996). In these experiments, the laboratory apparatus is arranged so as to be much "stiffer" than the experimental "fault" surfaces. The rate dependence of these friction laws refers to a dependence on logarithm of sliding velocity, and the state dependence to one or more state variables qi(t), each of which follows an independent relaxation equation.

2. Two classes of models have been developed and used that are based on laboratory observations, but are computationally simpler.

Coulomb-Amontons These are widely used because they are so simple (e.g., Rundle and Jackson, 1977; Nakanishi, 1991; Brown et al., 1991; Rundle and Brown, 1991; Rundle and Klein, 1992; Ben Zion and Rice, 1993, 1995, 1997). A static failure threshold, or equivalently a coefficient of static friction mS is prescribed, along with a residual strength, or equivalently a dynamic coefficient of friction mD. When the stress at a site increases, either gradually or suddenly, to equal or exceed the static value, a sudden jump in slip (change of state) occurs, that takes the local stress down to the residual value. These models naturally lend themselves to a Cellular Automaton (CA) method of implementation.

Velocity Weakening This model (Burridge and Knopoff, 1967; Carlson and Langer, 1989) is based on the observation that frictional strength diminishes as sliding proceeds. A constant static strength sf=sF is used as above, after which the assumption is made that during sliding, frictional resistance must be inversely proportional to sliding velocity.

3. Two classes of models are based on the use of statistical mechanics involving the physical variables that characterize stress accumulation and failure. Their basic goal is to construct a series of nonlinear stochastic equations whose solutions can be approached by numerical means:

Traveling Density Wave These models (Rundle et al., 1996; Gross et al., 1996) are based on the slip weakening model. The principle of evolution towards maximum stability is used to obtain a kinetic equation in which the rate of change of slip depends on the functional derivative of a Lyapunov functional potential. This model can be expected only to apply in the mean field regime of long range interactions, which is the regime of interest for elasticity in the Earth. Other models in this class include those of Fisher et al (1997) and Dahmen et al (1997).

Hierarchical Statistical Models. Examples include the models by Allègre et al. (1982, 1996); Smalley et al. (1985); Blanter et al. (1996); Allègre and Le Mouel (1994); Heimpel (1996); Newman et al. (1996); and Gross (1996). These are probabilistic models in which hierarchies of blocks or asperity sites are assigned probabilities of failure. As the level of external stress rises, probabilities of failure increase, and as a site fails, it influences the probability of failure of nearby sites.

4.4: Multipole Methods and Fast Numerical Simulation

4.4.1: Introduction

The GEM group has started to investigate the use of advanced parallel solvers for the codes described in section 3 developed by Rundle and Tullis. Here we consider for definiteness the Virtual_California code from Rundle. The Green’s function approach can be formulated numerically as a long-range all-pairs interaction problem and this can be straightforwardly parallelized using well-known algorithms. However one cannot reach the required level of resolution without switching from an order O(N2) to one of the O(N) or O(N logN) approaches. As in other fields, this can be achieved by dropping or approximating the long-range components and implementing a neighbor-list based algorithm. However it is more attractive to formulate the problem as interacting dipoles and adapt existing fast-multipole technology developed for particle dynamics problems. We have already produced a prototype general purpose "fast multipole template code" by adapting the very successful work of Salmon and Warren (1997). These codes have already simulated over 300 million gravitating bodies on a large distributed memory system (a 4500-processor subset of the ASCI "Red" machine), so we expect these parallel algorithms to scale efficiently up to the problem sizes needed by GEM.

4.4.2: Multipolar Representation of Fault Systems

A primary key to a successful implementation of GEM models of faults systems will be to utilize computationally efficient algorithms for updating the interactions between fault segments. Converting the Green's function integrals to sums, without truncation or approximation, would require O(N2) operations between earthquakes, and possibly more for segments of faults experiencing an earthquake. For quasistatic interactions, the Green's functions Tijkl and Gijk for linear elasticity have a simple time dependence. Moreover, the Green's functions for linear viscoelasticity and for linear poroelasticity can be obtained from the elastic Green's functions using the correspondence principle (e.g., Lee, 1955; Rundle 1982a,b). These simplifications strongly suggest that multipole expansions (Goil, 1994; Goil and Ranka, 1995) will be computationally efficient algorithms.

The stress and displacement Green's functions Tijkl and Gijk represent the tensor stress and vector displacement at x due to a point double couple located at x' (Steketee, 1958). The orientation at x' of the equivalent fault surface normal vector, and of the vector displacement on that fault surface, are described by the indices i and j. Displacement and stress indices at the field point x are described by indices k and l. Integration of Tijkl and Gijk over the fault surface then corresponds to a distribution of double couples. For that reason, representation of the stress over segments of fault in terms of a multipole expansion is the natural basis to use for the GEM computational problem. In fact, the use of multipolar expansions to represent source fields in earthquake and explosion seismology was introduced by Archambeau (1968) and Archambeau and Minster (1978), and later revisited from a different perspective by Backus and Mulcahy (1976). Minster (1985) gives a review of these early representations.

4.4.3: Application of Fast Multipole Methods to GEM

In the gravitational N-body problem, each body interacts with every other one in the system according to the familiar law of gravitational attraction. Simply computing all pairs of interactions requires N(N-1)/2 separate evaluations of the interaction law. This formulation of the problem has some important advantages: it is easy to code, it is easy to vectorize and parallelize, it is readily expressible in HPF, and it is even amenable to special-purpose hardware [e.g. GRAPE]. Nevertheless, even today's fastest special-purpose systems, running in a dedicated mode for extended times at rates of nearly 1 TERAFLOP, cannot simulate systems larger than about 100,000 bodies.

Tremendous computational savings may be realized by combining bodies into "cells" and approximating their external field with a truncated multipole expansion. When this idea is applied systematically, the number of interactions may be reduced to O(N logN) (Appel, 1985; Barnes and Hut, 1986) or O(N) (Greengard and Rokhlin, 1987; Anderson, 1992). The cells are generally arranged in a tree, with the root of the tree representing the entire system, and descendants representing successively smaller regions of space. Salmon and Warren (1997) have demonstrated that such codes can run in parallel on thousands of processors and have simulated highly irregular cosmological systems of over 300 million bodies using ASCI facilities.

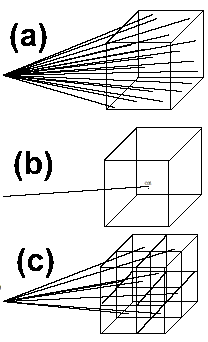
Fig. 12: Three ways of calculating long range forces

The basic idea of fast multipole methods is shown in the three versions of fig. 12. In 12(a), we show the simple O(N²) approach with a single particle on the left interacting with all the individual particles in a box on the right. The naïve computational simplification shown in fig. 12(b) is to replace (in the gravity case) the particles by their center of mass and use a single force calculation. However this approximation may not be accurate enough and so in fig. 12(c) we show the original box broken into 8 sub-boxes with the total summed over the individual sub-box contributions. This idea can be automated and implemented in a clever way so that the boxes used get smaller as you move closer to a given particle or if there is significant variation in particle density. Further there are subtle but very efficient parallel versions of the method to build the set of hierarchical sub-boxes (which form a tree so that these are often termed tree codes) which in the case of gravity is rebuilt each time step. In figure 13 below, we illustrate the adaptive division generated for 10,000 particles clustered in a two-dimensional disk.

Fig. 13: Adaptive division of disk of particles into cells

There is a direct analogy between the bodies in an astrophysical N-body system and the fault segments in a GEM. In both cases, there exists a pair-wise interaction that seems to require O(N2) interactions. But if we represent the distribution of sources in a region by a multipole expansion, the external field generated by a large number of bodies can be computed to any desired degree of accuracy in constant time. Thus, the GEM problem can also be reduced to O(NlogN) or O(N) total interactions, so that large calculations are tractable. On the other hand, although multipole methods can deliver large performance gains, they also require a considerable infrastructure. This is especially true of efficient parallel implementations. We intend to develop the multipole version of GEM using a library that has been abstracted from Salmon and Warren's successful astrophysical N-body codes. This new library is:

Modular - The "physics" is cleanly separated from the "computer science", so that in principle, alternative physics modules such as the evaluation of the GEM Green's functions, can simply be "plugged in". The first non-gravitational demonstration was a vortex dynamics code written by Winckelmans et al. (1995). The interface to the physics modules is extremely flexible. A general decision-making function tells the treecode whether or not a multipole, or any other approximation, is adequate for a given field evaluation. Short-range interactions, which vanish outside a given radius, can be handled as well.

Tunable - Careful attention to analytical error bounds has led to significant speed-ups of the astrophysical codes, while retaining the same level of accuracy. Analytic error bounds may be characterized as quantifying the fact that the multipole formalism is more accurate when the interaction is weak: when the analytic form of the fundamental interaction is well-approximated by its lower derivatives; when the sources are distributed over a small region; when the field is evaluated near the center of a "local expansion"; when more terms in the multipole expansion are used, and when the truncated multipole moments are small. These issues are primarily the concern of the "physics" modules, but the library provides a sufficiently powerful interface to make these parameters adjustable. The formulation is general enough that the same library can be used to support evaluation of O(N), O(NlogN) and O(N2) approximation strategies, simply by changing the decision criteria and interaction functions.

Adaptive - The tree automatically adapts to local variations in the density of sources. This can be important for GEM as it is expected that large earthquakes are the result of phenomena occurring over a wide range of length and time scales.

Scalable - The library has been successfully used on thousands of processors, and has sustained 170 Gflops aggregate performance on a distributed system of 4096 200Mhz PentiumPro processors.

Out of core - The library can construct trees, and facilitates use of data sets that do not fit in primary storage. This can allow one to invest hardware resources into processing rather than memory, resulting in more computations at constant resources.

Dynamically load balanced - The tree data structure can be dynamically load-balanced extremely rapidly by sorting bodies and cells according to an easily computed key.

Portable - The library uses a minimal set of MPI primitives and is written entirely in ANSI C. It has been ported to a wide variety of distributed memory systems - both 32-bit and 64-bit. Shared memory systems are, of course, also supported simply by use of an MPI library tuned to the shared memory environment.

Versatile - Early versions of the library have already been applied outside the astrophysics and molecular dynamics area. In particular the Caltech and Los Alamos groups have successfully used it for the vortex method in Computational Fluid Dynamics.

In the full GEM implementation, we have a situation similar to the conventional O(N2) N-body problem but there are many important differences. As the most obvious difference, the GEM case corresponds to double-couple interactions, which correspond to a different force law between "particles" from the gravitational case. Further the critical dynamics -- namely earthquakes -- are found by examining the stresses at each time step to see if the friction law implies that a slip event will occur. As discussed above, many different versions of the friction law have been proposed, and the computational system needs be flexible so we can compare results from different laws. Noting that earthquakes correspond to large-scale space-time correlations including up to perhaps a million 10-to-100 meter segments slipping together shows analogies with statistical physics. As in critical phenomena, clustering occurs at all length scales and we need to examine this effect computationally. However, we find differences with the classical molecular dynamics N-body problems not only in the dynamical criteria of importance but also in the dependence of the Green’s function (i.e. "force" potential) on the independent variables. Another area of importance, which is still not well understood in current applications, will include use of spatially dependent time steps (with smaller values needed in active earthquake regions). An important difference between true particles and GEM is that in the latter case, fault positions are essentially fixed in space. Thus the N-body gravitational problem involves particles whose properties are time-invariant but whose positions change with time, while GEM involves "particles" whose positions are fixed in time, but whose properties change with the surrounding environment. Of course a major challenge in both cases is the issue of time-dependent "clustering" of "particles." It may be possible to exploit this in the case of GEM - for example by incrementally improving parallel load balancing.

4.5: Computational Complexity

Current evidence suggests that forecasting earthquakes of magnitude ~6 and greater will depend upon understanding the space-time patterns displayed by smaller events; i.e., the magnitude 3's, 4's and 5's. With at least 40,000 km2 of fault area in southern California, as many as 108 grid sites (10-meter segment size) will be needed to accommodate events down to magnitude 3. Extrapolations based upon existing calculations indicate that using time steps of ~100 sec implies that ~108 time steps will be required to simulate several earthquake cycles. This leads to the need for teraflop class computers in this as in many physical simulations.

Here we make the conservative assumption that the GEM dipole-dipole Green's function evaluations are ten times as computationally expensive as the Newtonian Green's functions evaluated in Salmon and Warren's code. At this stage, we cannot guess how far the teraflop class of computer will take us and the systems needed to support research, crisis managers or insurance companies assessing possible earthquake risk, may require much higher performance.

4.6: Integration of Simulation Modules into GEMCI

As we described in section 2.5, we will adopt a hierarchical model for the simulation components used in GEMCI. The full Greens function programs would be macroscopic distributed objects which we can be manipulated by systems like WebFlow and linked with other coarse grain components such as sensor data, other programs such as finite-element solvers and visualization systems. These components are made up of smaller objects used in library fashion. Here we have the friction modules and different solver engines such as the conventional O(N²) and fast multipole methods with each having sequential and parallel versions. The latter would often exist in multiple forms including an openMP version for shared memory and MPI version for distributed memory.

5: Typical Computational Problems

Here we give three sample scenarios, which would correspond to distinct problem solving environments built using GEMCI.

5.1: Seismicity Models and Data Assimilation

Our first example of how the GEMCI might be used is drawn from an attempt to create a computer model of the seismicity of California or other seismically active region. Such a model, to the extent that it is realistic, could be quite useful in guiding intuition about the earthquake process, and suggesting new measurements or lines of inquiry.

Making such a model realistic requires many different types of data and there are for instance already substantial archives accumulated by the Southern California Earthquake Center (SCEC), as well as the Seismological Laboratory of the California Institute of Technology, and the Pasadena field office of the United States Geological Survey. The relevant data includes:

1. Broadband seismic data from the TERRASCOPE array
2. Continuous (SCIGN) and "campaign style" geodetic data
3. Paleoseismic data collected on the major faults of southern California
4. Near field strong motion accelerograms of recent earthquakes
5. Field structural geology of major active faults
6. Other data including GPS data, leveling data, pore fluid pressure, in situ stress, heat flow, downhole seismic data, multi-channel seismic data, laboratory measurements of mechanical properties of various rocks, 3-D geologic structure, gravity data, magneto-telluric data, hydrology data, and ocean tide data (to constrain coastal uplift).

. These will be used, for example, to update the fault geometry models used by GEM, and to update fault slip histories used to validate earthquake models.

A new and extremely promising type of geodetic data is Synthetic Aperture Radar Interferometry (InSAR), which permits "stress analysis of the Earth." A number of SAR missions are currently acquiring data over southern California, including the C-band (5.8 cm) European ERS 1/2 satellites and the L-band Japanese JERS satellite. These missions have already produced revolutionary images of the complete deformation fields associated with earthquakes in the United States and Japan (e.g., Massonnet et al., 1993). These techniques rely on radar interferograms that represent the deformation field at a resolution of a few tens of meters over areas of tens of thousands of square kilometers, and over time intervals of weeks to years. We are now able to see essentially the complete surface deformation field due to an earthquake, and eventually, due to the interseismic strain accumulation processes.

There are productive scientists who have built entire careers on each individual type of data mentioned above. No individual scientist at this time has access to complete collections of all these data types, nor the detailed expertise that would be required to use all these data in a computational model. Consequently, the traditional models are based on some subset of the data, with which we can try to predict other sets. However a more powerful approach can be based around an environment in which people can collaborate to construct and test models that span multiple data sets and which can then be embellished by other investigators.

To maximize the utility of any given data set, the people who collect and care about the data must be the ones who archive it and make it available. Attempts to construct monolithic databases of diverse earth science data using dedicated people and facilities have met with limited success. It appears to work better if the people or community who "own" the data are the ones who archive it. Thus, we need an environment, which will allow easy collaboration, and access to diverse distributed data sets. To return to our example of modeling the seismicity of California, an investigator might start with a map of faults in the region, a constitutive law for determining the slip on those faults derived from laboratory measurements, and some sort of loading criteria perhaps derived from GPS measurements. From these inputs, a model is constructed which reproduces the statistics of rupture as shown by paleoseismicity data and earthquake catalogs. Subsequently, another investigator takes that model and adds pore fluid pressure modeling in order to investigate the effects of fluids on the nucleation of earthquakes and the migration of seismicity. This process is repeated with other investigators collaborating and developing competing and/or complementary models. The models can be benchmarked against other data sets and against each other. This kind of an environment will enable us to make the most rapid possible progress at understanding the earthquake processes.

5.2: Response to an Earthquake in Southern California

This scenario is shown in the first part of fig. 14 with a prototype interface shown in figure 15. The goal is to rapidly form a consensus among researchers concerning the characterization of the deformation field and the location, size, and direction of slip on a fault following an earthquake. This consensus can be used to guide decisions on both civil and scientific responses to the quake.

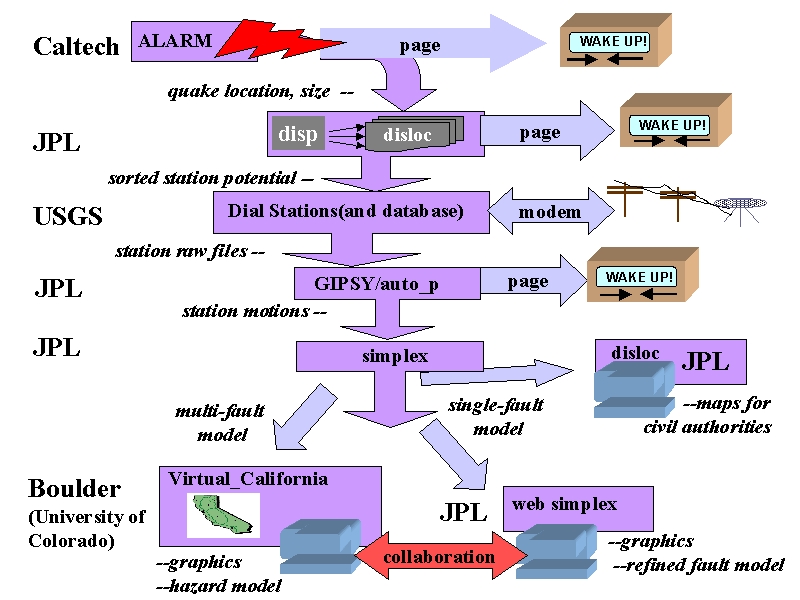
Fig. 14: Simulations used in Response to an Earthquake

Fig. 15: Computational structure of a fragment of the scenario in Fig. 14, which was implemented by NPAC as a prototype GEM Problem Solving Environment

Fig. 16: Desktop captured from a collaborative session such as that proposed in figs. 14 and 15.

This initial analysis is followed at the bottom of fig.14 by detailed simulations of the type described in section 4. We describe the whole process in detail below.

Following an earthquake in Southern California, the location and magnitude are calculated based on seismic data within minutes by Caltech/USGS, and currently are broadcast to several users via email and pagers. The information on location and magnitude could then be automatically used to define an area wherein instruments might be expected to record a signal. (the program disp) Data from these stations would be given priority in retrieval and analysis. In this example we will assume that the data in question is GPS data from the Southern California Integrated Geodetic Network (SCIGN) array. Retrieval in this case is done by telephone modem. As soon as the list of possibly affected stations has been generated, the database at the USGS is checked. If any of the stations on the list have not had data downloaded since the quake, computers at the USGS begin dialing the selected stations and retrieving the data.

Data from these stations would then be processed for rapid analysis to determine the measured displacements of the stations. (program GIPSY) If the measured displacements are large enough, emergency and scientific personnel are notified via email and pager. These displacements are then automatically fed into an inversion routine (program simplex) which solves for the best fit single fault displacement. This single fault displacement is in turn fed back into a forward elastic half space model, which yields a preliminary map of displacements over the whole area. (program disloc)

At this point this map is shared between various scientists and emergency personnel, using systems like Tango Interactive illustrated in figure 16 and described in section 6, that allow the collaboration and interaction of multiple people viewing and manipulating the same data set over the Internet. The emergency personnel can use the preliminary map in combination with a Geographical Information System data about utilities, lifelines, etc. to help assign resources to various areas. The scientists will use the preliminary map to help design a strategy for collecting additional measurements. They can also collaborate on refining the single fault model, possibly breaking the single preliminary fault into several segments, introducing more realistic material properties, or including more data, before rerunning the inversion.

This environment permits the rapid determination and dissemination of preliminary information about the earthquake and the collaborative refining of that information following an event. The rapid dissemination of information can greatly aid both the civil and scientific response to the quake. Resources can be more efficiently allocated to the areas where they are needed, and scientific measurements can be focused to provide information critical to refining our understanding of the earthquake system. Once an acceptable model of the earthquake has been determined, various models can be used to estimate the updated earthquake hazard for adjacent areas. Since there are currently several competing models for this it will undoubtedly involve multiple runs of multiple models and significant discussion among scientific colleagues. Each of these models as well as the various pieces of the automated processes described above have been developed by different people under different assumptions, and is developed, run, and maintained on computers under the control of the developer. The technologies such as CORBA and Enterprise Javabeans described in section 2, allow appropriate access and security mechanisms in this complex evolving distributed system.

The 1999 Izmit Turkey earthquake provided a recent example of how a system like this could have been useful. Following that earthquake, many geoscientists got together in a series of conference telephone calls to try to piece together what had happened, and what was an appropriate response. Some participants initially only knew what had been reported in the media. Others knew of specific pieces of data concerning the earthquake or of actions being taken by various groups and individuals. It is safe to say that no one had a complete picture. Much of the conference call was devoted to informing everyone about all the pieces of data and all the various initiatives that people were pursuing or might pursue. Similar calls and emails occurred after the 1992 Landers and 1994 Northridge earthquakes. Having a system such as has been described above wherein participants could share maps, descriptions, programs, data sets, and graphs and

wherein they could interactively and collaboratively manipulate the data and programs both synchronously and asynchronously would immeasurably aid the rapid and accurate diagnosis of what has happened and what should be done next.

5.3 Fundamental Computational Science Studies in Earthquake Forecasting

Above we described a relatively complicated real-time analysis scenario. Another important problem solving environment is that typically used in computational science to develop simulation codes, analysis techniques and run with multiple parameter values and compare with multiple data sets. This type of analysis has similarities with the previous two scenarios but now the collaboration for instance would not emphasis real-time issues so much but extend over many months or years. Technically this implies the need for powerful asynchronous tools linking over greater spans of time and space than the tightly coupled scenario of section 5.2. The tools needed here include the interactive rapid prototyping environment supporting pattern analysis and visualization. This aspect entails somewhat different trade-offs than the core simulations, in that interactivity is perhaps more critical than performance. As discussed in section 6, this could suggest that this part of the problem solving environment would be implemented client-side using interpretative languages. We would also need to experiment with many different ways of linking programs together and so we would have to support both program development and execution. The real-time constraints of section 5.2 would on the other hand emphasize execution of pre determined program modules.

This problem-solving environment would naturally link with that in section 5.1 as GPS, InSAR and broadband seismic (TERRASCOPE) data, together with archived and newly developed paleoseismic can be used in conjunction with the simulation capabilities to establish the relevant model parameters. These parameters include the current geometry of faults; slip rates on any given segment; recurrence intervals and historic variations in slip during earthquakes—leading to estimates of frictional parameters; deformation data leading to estimates of elastic plate thickness and sub-crustal stress; relaxation times; poroelastic stress relaxation in the crust following earthquakes, leading to estimates of drained and undrained elastic moduli; and variations in seismicity, leading to estimates of the variable properties of friction and fault geometry at depth. One must support the fitting of models to data with a suite of techniques (e.g., Menke, 1989), including least squares, evolutionary programming, and simulated annealing (Michalewicz, 1996; Holland, 1975; Rawlins, 1991), among others. In addition, one can expect to develop new methods so as to adapt models to assimilate new data as that becomes available, a concept that has served meteorological and climate studies extremely well. Self-adaptation techniques can be based on the same kinds of back-propagation methods that have been useful in analysis of neural network models (Hertz et al., 1991).

5.4: Seismic Waves and Earthquake Engineering

The most mature computations in the earthquake field are perhaps those used to calculate seismic waves and the corresponding response of buildings to them. In fact Clayton in the Caltech Geophysics department performed one of the very first Caltech Cosmic Cube computations to simulate the motion of earthquake waves in the Los Angeles Basin. This wave motion can in principle be generated from the earthquake "events" calculated in the Virtual_California simulations described in sections 4 and 5.3. These are large-scale finite element problems with complex grids and a recent NSF Grand Challenge project at CMU was very successful in this area [cmuquake]. The wave motion can be used as a forcing function for structural dynamics computations of buildings, roads and other civil infrastructure [curee].

6: Summary of GEMCI

We introduced in section 2.1 a computational environment GEMCI and described its overall framework in terms of distributed objects supported by commodity technologies like CORBA COM Java and XML. In the following sections we have discussed some especially important modules and how they are integrated into overall systems aimed at particular problem areas. Although we have not discussed them in detail, we will use some basic services, in particular security, collaboration and visualization. Security does not need much customization for computational science from the capabilities available from the commodity technologies for electronic commerce. Both Globus and Legion have developed good security approaches for high performance computing and GEMCI will be adopt such solutions. There is much experience in visualization in many projects although it is not clearly understood how to formulate this generally in systems like GEMCI. We can however expect that the substantial efforts by both Department of Energy and NSF will lead to visualization approaches appropriate for GEMCI. Collaboration corresponds to sharing of objects in GEMCI and this could correspond to shared rendering of data or the results of simulations. This technology is less mature than that for security and visualization although the Web has enabled powerful "asynchronous" collaboration where one posts information on web pages and your collaborators access your information at a later time. Synchronous collaboration can be important – especially in scenarios like those of section 5.2. Here approaches like Tango Interactive from NPAC at Syracuse [tango] are early prototypes that are expected to mature into powerful synchronously sharing for web pages and related data sets. An important area that we have not yet discussed in detail is the handling of data and its linkage to simulation. Here one of the leaders is the NSF NPACI partnership [npacidice] whose data-intensive activity is led by Reagan Moore. This approach makes extensive use of the same object standards advocated in GEMCI and we expect to be able to use the best available hardware and software to link data and simulations.

In summary, we believe that GEMCI has been designed to take advantages of the best available high performance and commodity information and simulation resources. We cannot predict the future of this rapidly changing field but GEMCI has made choices that should be able to track and exploit advances.

References

1) Allègre, C., J.L. Le Mouel and A. Provost, Scaling rules in rock fracture and possible implications for earthquake prediction, Nature, 297, 47-49, 1982.

2) http://shake2.earthsciences.uq.edu.au/ACES/ International collaboration within APEC for earthquake simulation

3) Ben-Zion, Y., Stress, slip and earthquakes in models of complex single-fault systems incorporating brittle and creep deformations, J. Geophys. Res., 101, 5677-5706, 1996.

4) Brown, S.R, C.J. Scholz and J.B. Rundle, A simplified spring-block model of earthquakes, Geophys. Res. Lett., 18, 2, 215-218, 1991.

5) Burridge, R and L. Knopoff, Model and theoretical seismicity, Bull. Seism. Soc. Am., 57, 341-371, 1967

6) Dieterich, J.H., A constitutive law for rate of earthquake production and its application to earthquake clustering, J. Geophys. Res., 99, 2601-2618, 1994.

7) Fisher, D. S., K. Dahmen, S. Ramanathan and Y. Ben-Zion, Statistics of earthquakes in Simple Models of Heterogeneous Faults, Phys. Rev. Lett., 78, 4885-4888, 1997.

8) Gabrielov, A., W. Newman and L. Knopoff, Lattice models of failure: Sensitivity to the local dynamics, Phys. Rev. E, 50, 188-197, 1994.

1. GEM web site (http://www.npac.syr.edu/projects/gem and http://milhouse.jpl.nasa.gov/gem/)

10) Jaume, S.C., and L.R. Sykes, changes in state of stress on the southern San Andreas Fault resulting from the California earthquake sequence of April to June 1992, Science, 258, 1325-1328, 1992.

11) Rundle, J.B., A physical model for earthquakes, 2, Application to southern California, J. Geophys. Res., 93, 6255-6274, 1988.

12) Rundle, J.B. and D.D. Jackson, Numerical simulation of earthquake sequences, Bull. Seism. Soc. Am., 67, 1363 - 1378, 1977.

13) Rundle, J.B. and W. Klein, New ideas about the physics of earthquakes, AGU Quadrennial report to the IUGG and Rev. Geophys. Space Phys., Supplement, July 1995, pp. 283-286.

14) Rundle, J.B., A physical model for earthquakes, 2, Application to Southern California, J. Geophys. Res., 93, 6255-6274, 1988.

15) Scholz, C.H., The Mechanics of earthquakes and Faulting, Cambridge University Press, Cambridge, U.K., 1990.

16) Tiampo, K., Rundle, J.B., W. Klein and S. Gross, Eigenpatterns in Southern California seismicity, submitted to Nature, 1999.

[SciAm] Jon Bosak and Tim Bray, XML and the Second-Generation Web, Scientific American May 99, http://www.sciam.com/1999/0599issue/0599bosak.html

[jini] http://www.sun.com/jini/

[ninja] http://ninja.cs.berkeley.edu/

[xsil] R.D. Williams, Caltech http://www.cacr.caltech.edu/SDA/xsil/index.html

[pdelab] E. N. Houstis, J. R. Rice, S. Weerawarana, A. C. Catlin, P. Papachiou, K. Y.

Wang, and M. Gaitatzes. PELLPACK: A Problem Solving Environment for

PDE Based Applications on Multicomputer Platforms. ACM Transaction on

Mathematical Software, 24:30-73, 1998. See http://www.cs.purdue.edu/research/cse/pdelab/pdelab.html

[Globus] Globus Metacomputing Toolkit, home page: http://www.globus.org

[GRAPE] http://grape.c.u-tokyo.ac.jp/gp/

[cmuquake] http://www.cs.cmu.edu/~quake/ (Jacobo Bielak and David O'Hallaron)

[gemhome] Reference 9 above

[pooma] http://www.acl.lanl.gov/ PoomaFramework/

[nile] (http://www.nile.utexas.edu/)

[legion] http://www.cs.virginia. edu/~legion/

[tango] http://www.npac.syr.edu/tango

[npacidice] http://www.npaci.edu/DICE/

[curee] http://www.curee.org/

From Final KDI 98 Proposal

BIBLIOGRAPHY

Aki, K. and P.G. Richards, Quantitative Seismology, Theory and Methods, vols I and II, W.H. Freeman, San Francisco, 1980.

Aki, K., Magnitude-frequency relations for small earthquakes: A clue to the origin of fmax of large earthquakes, J. Geophys. Res., 92, 1349-1355, 1987.

Allègre, C., J.L. Le Mouel and A. Provost, Scaling rules in rock fracture and possible implications for earthquake prediction, Nature, 297, 47-49, 1982.

Allègre, C.J. and J.L. Le Mouel, Introduction of scaling techniques in brittle fracture of rocks, Phys. Earth Planet Int., 87, 85-93, 1994.

Allègre, C.J., J.L. Le Mouel, H.D. Chau and C. Narteau, Scaling organization of fracture tectonics and earthquake mechanism, Phys. Earth Planet Int., in press, 1996.

Allen, M.P. and D.J. Tildsley, Computer Simulations of Liquids, Clarendon Press, Oxford, 1987.

Amit, D.J., Field Theory, the Renormalization Group, and Critical Phenomena, World Scientific, Philadelphia, 1984.

An, L-J., and C.G. Sammis, A cellular automaton for the growth of a network of shear fractures, Tectonopyhsics, 253, 247-270, 1996.

Anderson, C.R., SIAM J. Sci. Stat. Comp., 13, 923, 1992.

Appel, A W. , An efficient Program for Many-Body Simulation, SIAM J. Sci. Stat. Comp., 6, 85, 1985.

Appel, A.W.,SIAM Journal on Computing., 6, 85, 1985.

Archambeau, C.B. and J.B. Minster, Dynamics in prestressed media with moving phase boundarires: A continuum theory of failure in solids, Geophys. J. R. Astr. , 52, 65-96, 1978.

Archambeau, C.B., General theory of elastodynamic source fields, Rev. Geophys. Space Phys., 16, 241-288, 1968.

Arrowsmith, D.K. and C.M. Place, An Introduction to Dynamical Systems, Cambridge University Press, Cambridge, U.K., 1991.

Atkinson, B.K., Fracture Mechanics of Rock, Academic Press, London, 1987.

Backus, G and M. Mulcahy, Moment tensors and other phenomenological descriptions of seismic sources - I: Continuous displacements, Geophys. J. Roy. Astr. Soc., 46, 341-361, 1976.

Bak, P. and C. Tang, earthquakes as a self-organized critical phenomenon, J. Geophys. Res., 94, 15635-15638, 1989.

Bakun, W. and T.V. McEvilly, Recurrence models and Parkfield, California, earthquakes, J. Geophys. Res., 89, 3051-3058, 1984

Bakun, W.H. and A.G. Lindh, The Parkfield, California prediction experiment, earthquake Pred. Res., 3, 285-304, 1985.

Barnes, J. and Hut, P., Nature, 324, 446, 1986.

Barnes, J.E. and P Hut, A Hierarchical (O (N logN) ) Force-Calculation Algorithm, Nature, 324, 446-449, 1986.

Barnes-Hut Algorithm for {N}-Body Simulations, Supercomputing '94, IEEE Comp. Soc., Los Alamitos, 1994.

Beck, S.L. and D.H. Christensen, Ruture process of the February 4, 1965, Rat Islands earthquake, J. Geophys. Res., 96, 2205-2221, 1991.

Beck, S.L. and L.J. Ruff, The rupture process of the 1976 Mindanao earthquake, J. Geophys. Res., 90, 6773-6782, 1985.

Beck, S.L. and L.J. Ruff, The rupture process of the great 1979 Colombia earthquake: Evidence for the asperity model, J. Geophys. Res., 89, 9281-9291, 1984.

Beeler, N. and TE Tullis, Self healing slip pulses in dynamic rupture models due to velocity dependent strength, Bull. Seism. Soc, in press, 1996.

Beeler, N., TE Tullis and JD Weeks, The roles of time and displacement in the evolution effect in rock friction, Geophys. Res. Lett., 21, 1987-1990, 1994.

Beeler, N.M., T.E.Tullis, M.L. Blanpied and J.D. Weeks, Frictional behavior of large displacement experimental faults, J. Geophys. Res., 101, 8697-8715, 1996.

Ben-Zion, Y. and J. R. Rice, Dynamic simulations of slip on a smooth fault in an elastic solid, J. Geophys. Res., 102, 17771-17784, 1997.

Ben-Zion, Y. and J. R. Rice, earthquake failure sequences along a cellular fault zone in a three-dimensional elastic solid containing asperity and nonasperity regions, J. Geophys. Res., 98, 14109-14131, 1993.

Ben-Zion, Y. and J. R. Rice, Slip patterns and earthquake populations along different classes of faults in elastic solids, J. Geophys. Res., 100, 12959-12983, 1995.

Ben-Zion, Y., Stress, slip and earthquakes in models of complex single-fault systems incorporating brittle and creep deformations, J. Geophys. Res., 101, 5677-5706, 1996.

Ben-Zion, Y., V. Lyakhovsky and A. Agnon, Non Stationary Evolution of earthquakes and Faults in a Rheologically Layered Model of the Lithosphere, Spring AGU meeting, 1998.

Beroza, G.C., Near Source modeling of the Loma Prieta earthquake; evidence for heterogeneous slip and implications for earthquake hazard, Bull. Seismol. Soc. Amer., 81, 1603-1621, 1991.

Beroza, G.C., Seismic source modeling, US National Rept. to IUGG 1991-1994, Amer Geophys. Un., 1995., pp. 299-308.

Berryman, J.G. and G.W. Milton, Normalization constraint for variational bounds on fluid permeability, J. Chem. Phys., 83, 754-760, 1985.

Bilham, R. and P. Bodin, Influence of fault zone connectivity on segment slip rate: Boundary element estimates for the San Francisco Bay area, Science, 258, 281-284, 1992.

Binder, K., Applications of the Monte Carlo Method in Statistical Mechanics, vol. 36 of Topics in Current Physics, Springer-Verlag, Berlin, 1987.

Binder, K., Monte Carlo Methods in Statistical Physics, vol. 7 of Topics in Current Physics, Springer-Verlag, Berlin, 1986.

Blanter, EM, MG Schnirman, JL Le Mouel and C.J. Allgre, Scaling laws in block dynamics and dynamic self-organized criticality, Phys. Earth. Planet. Int., in press, 1996.

Board, J.A. , J W. Causey , J F. Leathrum, A. Windemuth and K. Schulten, Accelerated molecular dynamics simulation with the parallel fast multipole algorithm, Chem. Phys. Let., 198, 89, 1992

Brown, S. and G. Gruner, Charge and spin density waves, Sci. Amer., 270, 50-57, 1994.

Brown, S.R. and C. Scholz, Broad bandwidth study of the topography of natural rock surfaces, J. Geophys. Res., 90, 12575-12582, 1985.

Brown, S.R, C.J. Scholz and J.B. Rundle, A simplified spring-block model of earthquakes, Geophys. Res. Lett., 18, 2, 215-218, 1991.

Brune, J.N., S. Brown, and P.A. Johnson, Rupture mechanism and interface separation in foam rubber models of earthquakes; a possible solution to the heat flow paradox and the paradox of large overthrusts, Tectonophys., 218, 59-67, 1993.

Burridge, R. and C.A. Varga, The fundamental solution in dynamic poroelasticity, Geophys. J. Roy. astr. Soc., 58, 61-90, 1979.

Carlson, J.M and J.S. Langer, Properties of earthquakes generated by fault dynamics, Phys. Rev. Lett., 62, 2632-2635, 1989.

Carlson, J.M., J.S. Langer, B.E. Shaw and C. Tang, Intrinsic properties of a Burridge-Knopoff model of an earthquake fault, Phys. Rev. A, 44, 2, 884-897, 1991a.

Carlson, J.M., Time intervals between characteristic earthquakes and correlations with smaller events; an analysis based on a mechanical model of a fault, J. Geophys. Res., 96, 4255-4267, 1991b.

Chen, G. and H. Spetzler, Complexities of rock fracture and rock friction from deformation of Westerly granite, PAGEOPH, 140, 95-119, 1993a.

Chen, G. and H. Spetzler, Topographic characteristics of laboratory induced shear fractures, PAGEOPH, 140, 123-135, 1993b.

Cleary, M.P., Fundamental solutions for a fluid-saturated porous solid, Int. J. Solids Str., 13, 785-806, 1977.

Coniglio, A. and W. Klein, J. Phys. A, 12, 2775, 1980.

Constantin, P., "Integral and Inertial Manifolds for Dissipative Partial Differential Equations", Springer-Verlag, 1989.

Cornell, C.A., S.-C. Wu, S.R. Winterstein, J.H. Dieterich, and R.W. Simpson, Seismic hazard induced by mechanically interactive fault segments, Bull. Seism. Soc.Am., 83, 436-449, 1993

Crutchfield, JP and BS McNamara, Equations of motion from a data series, Complex Systems, 1, 417-452, 1987.

Crutchfield, JP and JE Hanson, Turbulent Pattern Bases for Cellular Automata, Physica D, 69, 279 - 301, 1993.

Crutchfield, JP and K Young, Inferring statistical complexity, Phys. Rev. Lett., 63, 105-108, 1989.

Crutchfield, JP and K. Kaneko, Are attractors relevant to turbulence?, Phys. Rev. Lett., 60, 2715, 1988.

Crutchfield, JP, Subbasins, portals and mazes: Transients in high dimensions, J. Nucl. Phys. B., 5A, 287, 1988.

Crutchfield, JP, The calculi of emergence: Computation, dynamics, and induction, Physica D, 75, 11-54, 1994.

Das, S., J. Boatwright, and C.H. Scholz, eds., earthquake Source Mechanics, Maurice Ewing vol. 6, Geophys. Monog. 37, Amer. Geophys. Un., Washington, DC, 1986.

de Sousa Vieria, M., G.L. Vasconcelos and S.R. Nagel, Dynamics of spring-block models: Tuning to criticality, Phys. Rev. E, 47, 4, R2221-2224, 1993.

Dieterich, J.H. and M.F. Linker, Fault stability under conditions of variable normal stress, Geophys. Res. Lett., 19, 16, 1691-1694, 1992

Dieterich, J.H., A constitutive law for rate of earthquake production and its application to earthquake clustering, J. Geophys. Res., 99, 2601-2618, 1994.

Dieterich, J.H., Constitutive properties of rock with simulated gouge, In Mechanical Behavior of Crustal Rocks. AGU Geophys. Monograph 24, Washington, DC, American Geophysical Union, 103-120, 1981.

Dieterich, J.H., Time dependent friction and the mechanics of stick slip, Pure Appl. Geophys., 116, 790-806, 1978.

Dieterich, J.H., Time dependent friction in rocks, J. Geophys. Res., 77, 3690-3697, 1972

Ding, E.J. and Y.N. Lu, Analytical treatment for a spring-block model, Phys. Rev. Lett., 70, 3627-3630, 1993.

Ding, H.-Q. and N. Karasawa and W.A. Goddard, Atomic Level Simulations of on a Million Particles: The Cell Multipole Method for Coulomb and London Interactions, J. of Chemical Physics, 97, 4309-4315, 1992

Dmowska, R. and L. Lovison, Influence of asperities along subduction interfaces on the stressing and seismicity of adjacent areas, Tectonophysics, 211, 23-41, 1992.

Dowla, F.U., T.F. Hauk, J.B. Rundle and J.J.Hopfield, earthquake forecasting using neural networks (abstr.), Seism. Res. Lett., 63, 21, 1992.

Eberhart-Phillips, D. and A.J. Michael, Three-dimensional velocity structure, seismicity, and fault structure in the Parkfield region, central California, J. Geophys. Res., 98, B9, 15737-15758, 1993.

Eneva, M. and Y. Ben-Zion, Application of pattern recognition techniques to earthquake catalogs generated by models of segmented fault systems in three-dimensional elastic solids, J. Geophys. Res., 102, 24513-24528, 1997a.

Eneva, M. and Y. Ben-Zion, Techniques and parameters to analyze seismicity patterns associated with large earthquakes, J. Geophys. Res., 102, 17785-17795, 1997b.

Engdahl, E.R., S. Billington, and C. Kisslinger, Teleseismically recorded seismicity before and after the May 7, 1986 Andreanof Islands, Alaska, earthquake, J. Geophys. Res., 94, 15481-15498, 1989.

Feynman, R.P. and A.R. Hibbs, Quantum Mechanics and Path Integrals, McGraw-Hill, New York, 1965.

Fisher, D. S., K. Dahmen, S. Ramanathan and Y. Ben-Zion, Statistics of earthquakes in Simple Models of Heterogeneous Faults, Phys. Rev. Lett., 78, 4885-4888, 1997.

Fisher, DSPhys. Rev. B., 31, 1396 (1985)

Foley, J., van Dam, A., Feiner, S., and Hughes, J., Computer Graphics, Principles and Practice, 550, (Reading, MA Addison-Wesley), Reading, MA. 1990.

Fortuin, C.M. and P.W. Kasteleyn, Physica, (Utrecht), 57, 536, 1972.

Fox, G.C., W. Furmanski , Snap, Crackle, WebWindows! , http://www.npac.syr.edu/techreports/html/0750/abs-0758.html , 1996

Fox, G.C., R.D. Williams, and P.C. Messina, Parallel Computing Works!, Morgan Kauffman, San Francisco, 1994.

Frisch, U., Turbulence, The Legacy of A.N. Kolmagorov, Cambridge Unviersity Press, Cambridge, UK, 1995.

G.C. Fox, GC, W. Furmanski, M. Chen, C. Rebbi, J. Cowie, WebWork: Integrated Programming Environment Tools for National and Grand Challenges, http://www.npac.syr.edu/techreports/html/0700/abs-0715.html, 1995

Gabrielov, A., W. Newman and L. Knopoff, Lattice models of failure: Sensitivity to the local dynamics, Phys. Rev. E, 50, 188-197, 1994.

Goil, S. and S. Ranka, Parallelization of heirarchically structured applications on distributed memory machines, NPAC Tech Rept. SCCE-688, http:/www.npac.syr.edu/techreports/index.html, 1995.

Goil, S., Primatives for problems using heirarchical algorithms on distributed memory machines, NPAC Tech Rept. SCCS-687, http:/www.npac.syr.edu/techreports/index.html, 1994.

Goldberg, D.E., Genetic Algorithms in Search, Optimization, and Machine Learning, Addison Wesley, Reading, MA, 1989.

Gopal, A,D. and D.J. Durian, Phys. Rev. Lett., 75, 2610 (1995).

Grama, A. V. Kumar and Ahmed Sameh, Scalable Parallel Formulations of the

Grant, L. and A. Donnellan, 1855 and 1991 surveys of the San Andreas fault: Implications for fault mechanics, Bull. Seism. Soc. Am., 84, 241-246, 1994.

Grant, L. and K. Sieh, Paleoseismic evidence of clustered earthquakes on the San Andreas fault in the Carrizo Plain, J. Geophys. Res., 99, 6819-6842, 1994.

Grassberger, P., Phys. Rev. E., 49, 2436, 1994.

Greengard, L. and Rokhlin, V., J. Comp. Phys, 73, 325-348, 1987.

Gross, S., J.B. Rundle and W. Klein, Simulations of the Traveling Density Wave model for earthquakes and comparison to observations, preprint, 1996

Gross, S., On the scaling of average slip with rupture dimensions of earthquakes, pp.157-166 in JB Rundle, D. Turcotte and W. Klein, eds., Reduction and Predictability of Natural Disasters, vol XXV in the Santa Fe Inst. series on the Sciences of Complexity, Addison Wesley, 1996.

Haberman, R.E., Consistency of teleseismic reporting since 1963, Bull. Seism. Soc. Am., 72, 93-111, 1982.

Hanks, T.C., Small earthquakes, tectonic forces, Science, 256, 1430-1432, 1992.

Hanson, J.E. and J.P. Crutchfield, The attractor-basin portrait of a cellular automaton, J. Stat. Phys., 66, 1415-1462, 1992.

Harris, R.A., and R.W. Simpson, Changes in static stress on Southern California faults after the 1992 Landers earthquake, Nature (London), 360, 251-254, 1992.

Heaton, T., Evidence for and implications of self-healing pulses of slip in earthquake rupture, Phys. Earth and Planet. Int., 64, 1-20, 1990.

Heaton, T.H., Evidence for and implications for self-healing pulses of slip in earthquake rupture, Phys. Earth Planet. Int., 64, 1-20, 1990.

Heimpel, M., earthquake size-frequency relations from an analytical stochastic rupture model, J. Geophys. Res., in press, 1996.

Hernquist, L. and N. Katz,{TREESPH} - A Unification of {SPH} with the Hierarchical Tree Method, Astrophysical J. Supp., 70, 419, 1989

Hertz, J. , A. Krogh and R.G. Palmer, Introduction to the Theory of Neural Computation, Lecture Notes I, Santa Fe Inst. Addison Wesley, Reading, MA, (1991).

A.V.M. Herz and J.J. Hopfield, Phys. Rev. Lett., 75, 1222 (1995).Herz, A.V.M. and J.J. Hopfield, Rapid phase locking in coupled integrate-and-fire neurons, preprint, 1995.

Hill, D.P., and others, Seismicity remotely triggered by the magnitude 7.3 Landers, California, earthquake, Science , 260, 1617-1623, 1993.

Hill, R. A self consistent mechanics of composite materials, J. Mech.. Phys. Sol., 13, 213-222, 1965.

Holland, J.H., Adaptation in natural and artificial systems, University of Michigan Press, Ann Arbor, 1975.

Holt, C. and J P Singh, Hierarchical {N}-body methods on shared address space multiprocessors , SIAM, Seventh SIAM Conference on Parallel Processing for Scientific Computing, Philadelphia, 1995.

Hopfield, J.J., Neurons, dynamics and computation, Physics Today, 47, 40-46, 1994.

Hu, Y. and S. L. Johnsson, A Data Parallel Implementation of Hierarchical {N}-body Methods, Harvard University, TR-26-94, 1994.

Huang, J. and D.L. Turcotte, Chaotic seismic faulting with a mass-spring model and velocity weakening friction, PAGEOPH, 138, 570-589, 1992.

Huang, J., G. Narkounskaia and D.L. Turcotte, A cellular-automata, slider-block model for earthquakes, II. Demonstration of self-organized criticality for a 2-D system, Geophys. J. Int., 111, 2, 259-269, 1992.

Huang, Y., H. Saleur, C. Sammis, and D. Sornette, Precursors, aftershocks, criticality and self-organized criticality, Europhys. Letters , 41, 43-48, 1998.

Ihmle, P.F., P. Harabaglia and T.J. Jordan, Teleseismic detection of a slow precursor to the great 1989 Macquarie Ridge earthquake, Science, 261, 5118, 177-183, 1993.

Ivins, E.R. and C.G. Sammis, On lateral viscosity contrast in the mantle and the rheology of low frequency geodynamics, Geophys. J. Int, in press, 1995b.

Ivins, E.R., Composite Constitutive Theory for a Solid Earth of Strong Lateral Viscosity Contrast, Ph.D. Dissertation, Univ. Southern Calif., 1995a.

Jackson, D.D. and others, Seismic hazards in southern California: Probable earthquakes, 1994 to 2024, Bull. Seism. Soc. Am., 85, 379-439, 1995.

Jaume, S.C., and L.R. Sykes, changes in state of stress on the southern San Andreas Fault resulting from the California earthquake sequence of April to June 1992, Science, 258, 1325-1328, 1992.

Johnson, P.A., M. Antolik, W.A. Peppin, W. Foxall, and T.V. McEvilly, Structure and rupture processes of the fault zone at Parkfield from the spectra of microEarthquakes, Seism. Res. Lett., 63, 75, 1992.

Jordan, T.H., Far-field detection of slow precursors to fast seismic ruptures, Geophys. Res. Lett., 18, 11,2019-2022, 1991.

Kagan, Y.Y., and D.D. Jackson, Seismic gap hypothesis; ten years after, J. Geophys. Res., 96, 21419-21431, 1991.

Kalia, R.K., S. de Leeuw, A. Nakano and P. Vashishta, Molecular dynamice simulations of Coulombic systems on distributed-memory {MIMD} machines}, Comput. Phys. Commun., 74, 316-326, 1993.

Kanamori, H, Global seismicity, pp. 596-608 in earthquakes: Observation, Theory and Interpretation, Course LXXXV, Proc. Intl. School of Physics "Enrico Fermi", the Italian Physical Society, North Holland, Amsterdam, 1983.

Kanamori, H. and D.L. Anderson, Theoretical basis for some empirical relations in seismology, Bull. Seism. Soc. Am., 65, 1073-1095, 1975.

Kanamori, H. and M. Kikuchi, The 1992 Nicaragua earthquake: A slow tsunami earthquake associated with subducted sediments, Nature, 361, 6414, 714-716, 1993.

Kanamori, H., E. Hauksson, A slow earthquake in the Santa Maria Basin, California, Bull. Seismol. Soc. Amer., 85, 2087-2096, 1992.

Kanamori, H., Mechanics of earthquakes, Ann. Rev. Earth Planet. Sci., 21, 1993.

Karageorgi, E., R. Clymer and T.V. McEvilly, Seismological studies at Parkfield, II. Search for temporal variations in wave propagation using Vibroseis, Bull. Seism. Soc. Amer., 82, 3, 1388-1415, 1992.

Kikuchi, M., H. Kanamori and K. Satake, Source complexity of the 1988 Armenian earthquake: Evidence for a slow after-slip event, J. Geophys. Res., 98, B9, 15797-15808, 1993.

King, G. C. P., R. S. Stein, and J. Lin, Static stress changes and the triggering of earthquakes, Bull. Seismol. Soc. Amer., 84, 935-953, 1994.

King, G.C.P. and J. Nabelek, Role of fault bends in the initiation and termination of earthquake ruptureScience, 228, 984-987, 1985.

Kisslinger, C., The stretched exponential function as an alternative model for aftershock decay rate, J. Geophys. Res., 98, 1913-1921, 1993.

Klein, W. and F. Leyvraz, Crystalline nucleation in deeply quenched systems, Phys. Rev. Lett., 57, 2845-2848, 1986.

Knopoff, L., J.A. Landoni, and M.S. Abinante, Dynamical model of an earthquake fault with localization, Phys. Rev. A467, 7445-7449, 1992.

Kostrov, BV, Self similar problems of propagation of shear cracks, J. Appl. Mech., 28, 1077-1087, 1964.

Kostrov, B.V. and S. Das, Principles of Earthquake Source Mechanics, Cambridge University, Cambridge UK, 1988.

Lake, G., N. Katz, T Quinn and J Stadel, Cosmological {N}-body Simulation, SIAM, Seventh SIAM Conference on Parallel Processing for Scientific Computing, Philadelphia, 1995

Lay, T., H. Kanamori, and L. Ruff, The asperity model and the nature of large subduction zone earthquakes, earthquake Prediction Research, 1, 3-71, 1982.

Lees, J.M., and C. Nicholson, Three-dimensional tomography of the 1992 southern California earthquake sequence: constraints on dynamic earthquake rupture?, Geology, 21, 387-390, 1993.

Li, V.C., Mechanics of shear rupture applied to earthquake zones, in Fracture Mechanics of Rock, ed. B.K. Atkinson, Academic Press, London, 1987, pp. 351-428.

Linde, A.T., M.T. Gladwin, and J.J.S. Johnston, The Loma Prieta earthquake, 1989 and Earth strain tidal amplitudes; an unsuccessful search for associated changes, Geophys. Res. Letts., 19, 317-320, 1992.

Lomnitz-Adler, J., Automaton models of seismic fracture: constraints imposed by the magnitude-frequency relation, J. Geophys. Res., 98, 17745-17756, 1993.

Lyakhovsky, V., Y. Ben-Zion and A. Agnon, Distributed Damage, Faulting, and Friction, J. Geophys. Res., 102, 27635-2764, 1997.

Ma, S.-K., Modern Theory of Critical Phenomena, Benjamin-Cummings, Reading MA, 1976.

Ma, S.-K., Statistical Mechanics, World Scientific, Philadelphia, PA, 1985.

Marone, C.J., C.H. Scholz, and R. Bilham, On the mechanics of earthquake afterslip, J. Geophys. Res., 96, 8441-8452, 1991.

Maruyama, T., Fluid pressure responses of a water-saturated porous elastic multilayered half space to water pumping and atmospheric loading, J. Phys. Earth, 42, 331-375, 1994.

McNally, K.C., Plate subduction and prediction of earthquakes along the Middle America Trench, in earthquake Prediction, An International Review, AGU monograph 4, American Geophysical Union, Washington, DC, 1981.

Mendoza, C., Hartzell, S. and T. Monfret, Wide-band analysis of the 3 March, 1985 Central Chile earthquake: Overall source process and rupture history, Bull. Seism. Soc. Am., 84, 269-283, 1994.

Michalewicz, Z., Genetic Algorithms+Data Structures=Evolution Programs, Springer-Verlag, New York, 1996.

Minster, J.-B., Twenty five years of sesimic source theory, in The VELA Program, A Twenty-Five Year Review of Basic Research, ed. A.U. Kerr, Defense Advanced Research Projects Agency, pp. 67-116, 1985.

Monette, L. and W. Klein, Spinodal nucleation as a coalescence process, Phys. Rev. Lett., 68, 2336-2339, 1992.

Mora, P. and D. Place, Simulation of the frictional stick slip instabilty, Pure Appl. Geophys., 143, 61-87, 1994.

Mouritsen, O.G., in Computer Studies of Phase Transitions and Critical Phenomena, Springer-Verlag, Berlin, 1984.

Nadeau, R., M. Antolik, P.A. Johnson, W. Foxall and T.V. McEvilly, Seismological studies at Parkfield III: MicroEarthquake clusters of fault zone dynamics, Bull. Seism. Soc. Am., 84, 247-263, 1994.

Nakanishi, H., Cellular automaton model of earthquakes with deterministic dynamics, Phys. Rev. A, 43, 6613-6621, 1990.

Narkounskaia, G., and D.L. Turcotte, A cellular-automata, slider-block model for earthquakes; I, Demonstration of chaotic behaviour for a low order system, Geophys. J. Internat., 11, 250-258, 1992.

Narkounskaia, G., J. Huang and D.L. Turcotte, Chaotic and self-organized critical behavior of a generalized slider block model, J. Stat. Phys., 67, 1151-1183, 1992.

Narkounskaia, G., J. Huang and D.L. Turcotte, Chaotic and self-organized critical behavior of a generalized slider block model, J. Stat. Phys., 67, 1151-1183, 1992.

Newman, W.I. and A.M. Gabrielov, Failure of hierarchical distributions of fiber bundles, Int. J. Fracture, 50, 1-14, 1991.

Newman, W.I., AM Gabrielov, TA Durand, SL Phoenix and D.L. Turcotte, An exact renormalization model for earthquakes and material failure. Statics and dynamamics, Physica, D77, 200-216, 1994.

Newman, W.I., D.L. Turcotte and A. Gabrielov, A hierarchical model for precursory seismic activation, pp. 243-260, in J.B. Rundle, D.L. Turcotte and W. Klein, Reduction and Predictability of Natural Disasters, vol. XXV in the Santa Fe Institute series on complexity, Addison Wesley, 1996.

Nishenko, S.P., L.R. Sykes, D.D. Jackson, and Y.Y. Kagan, Seismic gap hypothesis; ten years after [discussion and reply], J. Geophys. Res., 908, 9909-9920, 1993.

Okada, Y., Internal deformation due to shear and tensile faults in a half-space, Bull. Seism. Soc. Am., 82, 1018-1040, 1992.

Okada, Y., Surface deformation duei to shear and tensile faults in a half-space, Bull. Seism. Soc. Am., 75, 1135-1154, 1985.

Olami, Z., H.J.S. Feder, and K. Christensen, Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes, Phys. Rev. Lett., 68, 1244-1247, 1992 (Comment by W. Klein and J. Rundle, Phys. Rev. Lett., 71, 1288, 1993, with reply by Christensen, Phys. Rev. Lett., 71, 1289, 1993)

Pacheco, J.F., C.H. Scholz, and L.R. Sykes, Changes in frequency-size relationship from small to large earthquakes, Nature (London), 355, I 71-73, 1992.

Pepke, S.L., J.M. Carlson and B.E. Shaw, Prediction of large events on a dynamical model of a fault, J. Geophys. Res., 99, 6769-6788, 1994.

Perrin, G.O., J.R. Rice and G. Zheng, Self-healing slip pulse on a frictional surface, J. Mech. Phys. Sol, 43, 1461-1495, 1995.

Place, D and P. Mora, Large scale simulations of the physics of earthquakes, Trans. Am. Geophys. Un. EOS, v. 76 Suppl., F424, 1995.

Power, WL, T. Tullis and JD Weeks, Roughness and wear during brittle faulting, J. Geophys. Res., 93, 15268-15278, 1988.

Rabinowicz, E., Friction and Wear of Materials, John Wiley, New York, 1965.

Rawlins, G.J., Foundations of Genetic Algorithms, Morgan-Kaufman publishers, San Francisco, 1991.

Reid, HF, in A.C. Lawson, The California earthquake of April 18, 1906, Report of the State earthquake Investigation Commission, Vol I (Carnegie Institution of Washington, Washington, DC, 1908).

Reynders, J. V. W. , D. W. Forslund, P. J. Hinker, M. Tholburn, D. G. Kilman, and W. F. Humphrey, Object-Oriented Particle Simulation on Parallel Computers, OON-SKI '94 Proceedings.

Reynders, J. V. W., D. W. Forslund, P. J. Hinker, M. Tholburn, D. G. Kilman, and W. F. Humphrey, OOPS: An Object-Oriented Particle Simulation Class Library for Distributed Architectures, Computer Physics Communications, 87, 212, 1995.

Reynders, J. V. W., J. C. Cummings, P. J. Hinker, M. Tholburn, M. Srikant, S. Banerjee, S. Atlas, K. Kaehy, POOMA: a FrameWork for Scientific Applications`` [to appear in `` Parallel Computing in C++, MIT Press, 1996.

Reynders, J. V. W., P.J. Hinker, J.C. Cummings, et al., POOMA: A Framework for Scientific Simulations on Parallel Architectures, Proceedings of the 1995 Computational Sciences Workshop, University of New Mexico (in press).

Rice J. R. and Y. Ben-Zion, Slip complexity in earthquake fault models, Proc. Natl. Acad. Sci. U.S.A, 93, 3811-3818, 1996.

Rice, J.R. and A.L. Ruina, Stability of steady frictional slipping, J. Appl. Mech., 105, 343-349, 1983.

Rice, J.R. and J.C. Gu, earthquake aftereffects and triggered seismic phenomena, Pure Appl. Geophys., 121, 443-475, 1983.

Rice, J.R. and M.Cleary, Some basic stress diffusion solutions for fluid saturated elastic porous media with compressible constituents, Rev. Geophys. Space Phys., 14, 227-241, 1976.

Rice, J.R. and S. T. Tse, Dynamic motion of a single degree of freedom system following a rate and state dependent friction law, J. Geophys. Res, 91, 521-530, 1986.

Rice, J.R. and W.D. Stuart, Stressing in and near a strongly coupled subduction zone during the earthquake cycle,(abstract), EOS Trans. Am Geophys. Un., 70, (43), 1063, 1989.

Rice, J.R. and Y. Ben-Zion, Slip complexity in earthquake fault models, Proc. Nat. Acad. Sci.USA, in press, 1996.

Rice, J.R., Spatio-temporal complexity of slip on a fault, J. Geophys. Res., 98, 9885-907, 1993.

Rice, J.R., The mechanics of earthquake rupture, in Physics of the Earth's Interior, ed. A.M. Dziewonski and E. Boschi, pp. 555-649, North-Holland, New York, 1980.

Richter, C.F., Elementary Seismology, W.H. Freeman, San Francisco, 1958.

Robertson, M.C., C.G. Sammis, M. Sahimi, and A. Martin, The 3-D spatial distribution of earthquakes in southern California with a percolation theory interpretation, J. Geophys. Res., 100, 609-620, 1995.

Rokhlin, V., Rapid Solution of Integral Equations of Classical Potential Theory, J. Comp. Phys., 60, 187--207, 1985.

Romanowicz, B. and J. B. Rundle, On scaling relations for large earthquakes, Bull.Seism. Soc. Am., 83, 1294-1297, 1993.

Romanowicz, B., Strike-slip earthquakes on quasi-vertical transcurrent faults: Inferences for general scaling relations, Geophys. Res. Lett., 19, 481-484, 1992.

Rudnicki, J.W., J. Yin, and E.A. Roeloffs, Analysis of water level changes induced by fault creep at Parkfield, California, J. Geophys. Res., 98, 8143-8152, 1993.

Ruff, L.J., Asperity distributions and large earthquake occurrence in subduction zones, Tectonophys., 211, 61-83, 1992.

Ruff, L.J., Fault asperities inferred from seismic body waves, pp. 251-276, in earthquakes: Observation, Theory and Interpretation, Course LXXXV, Proc. Intl. School of Physics "Enrico Fermi", the Italian Physical Society, North Holland, Amsterdam, 1983.

Rundle, J.B. and D.D. Jackson, Numerical simulation of earthquake sequences, Bull. Seism. Soc. Am., 67, 1363 - 1378, 1977.

Rundle, J.B. and D.L. Turcotte, New directions in theretical studies of tectonic deformation: A survey of recent progress, in Contributions of Space Geodesy to Geodynamics: Crustal Dynamics, ed. D.E. Smith and D.L. Turcotte, Geodynamics Ser. Vol. 23, AGU, Washington, DC, 1993.

Rundle, J.B. and S.R. Brown, Origin of rate dependence in frictional sliding, J. Stat. Phys., 65, 403-412, 1991.

Rundle, J.B. and W. Klein, Implications of a "toy" slider block model for the rupture mechanics of earthquakes, J. Geophys. Res., submitted, 1994 (also Trans. Am. Geophys. Un. EOS Fall meeting suppl. abstr., 405, 1993)

Rundle, J.B. and W. Klein, New ideas about the physics of earthquakes, AGU Quadrennial report to the IUGG and Rev. Geophys. Space Phys., in press, 1994.

Rundle, J.B. and W. Klein, Nonclassical nucleation and growth of cohesive tensile cracks, Phys. Rev. Lett., 63, 171-174, 1989.

Rundle, J.B. and W. Klein, Nonlinear dynamical models for earthquakes and frictional sliding: An overview, Proc. 33rd Symposium Rock Mech., A.A. Balkema, Rotterdam, 1992.

Rundle, J.B. and W. Klein, Scaling and critical phenomena in a class of slider block cellular automaton models for earthquakes, J. Stat. Phys., 72, 405-412, 1993.

Rundle, J.B., A physical model for earthquakes, 2, Application to southern California, J. Geophys. Res., 93, 6255-6274, 1988.

Rundle, J.B., A physical model for earthquakes: 1, Fluctuations and interactions, J. Geophys. Res., 93, 6237-6254, 1988.

Rundle, J.B., A physical model for earthquakes: 3, Thermodynamical approach and its relation to nonclassical theories of nucleation, J. Geophys. Res., 94, 2839-2855, 1989.

Rundle, J.B., Derivation of the complete Gutenberg-Richter magnitude-frequency relation using the principle of scale invariance, J. Geophys. Res., 94, 12337-12342, 1989.

Rundle, J.B., K. Tiampo and W. Klein, Recurring patterns in a realistic earthquake fault system model, preprint, 1998b.

Rundle, J.B., Magnitude frequency relations for earthquakes using a statistical mechanical approach, J. Geophys. Res., 98, 21943-21949, 1993.

Rundle, J.B., Some solutions for static and pseudo-static deformation in layered nonisothermal media, J. Phys. Earth, 30, 421-440, 1982b.

Rundle, J.B., Viscoelastic crustal deformation from a rectangular fault in a layered Earth, J. Geophys. Res., 87, 7787-7796, 1982a.

Rundle, J.B., W. Klein and K. Tiampo, Linear pattern dynamics in nonlinear threshold systems, Phys. Rev. Lett., submitted, 1998a.

Rundle, J.B., W. Klein and S. Gross, Dynamics of a Traveling Density Wave model for earthquakes, Phys. Rev. Lett., 76, 4285-4288, 1996.

Rundle, J.B., W. Klein and S. Gross, Dynamics of a traveling density wave model for earthquakes, Phys. Rev. Lett., 76, 4285-4288, 1996.

Rundle, J.B. and W. Klein, Dynamcal segmentation and rupture patterns in a "toy" slider block model for earthquakes, Nonlin. Proc. Geophys., 2, 61-81, 1995a.

Rundle, J.B., W. Klein, S. Gross and D.L. Turcotte, Boltzmann fluctuations in numerical simulations of nonequilibrium lattice threshold systems, Phys. Rev. Lett., 75, 1658-1661,1995b.

Rundle, JB, DL Turcotte and W. Klein, eds., Reduction and Predictability of Natural Disasters, Proc. Vol XXV, Santa Fe Inst. Ser. Complexity, Addison Wesley, Reading, MA, 1996.

Sahimi, M., M.C. Robertson and C.G. Sammis, Fractal distribution of earthquake hypocenters and its relation to fault patterns and percolation, Phys. Rev. Lett., 70, 2186-2189, 1993.

Saleur, H., C.G. Sammis, and D. Sornette, Discrete scale invariance, complex fractal dimensions, and log-periodic fluctuations in seismicity, J. Geophys. Res., 101, 17,661-17,677, 1996.

Salmon, J.K. and M. S. Warren. J. Comp. Phys., Skeletons from the treecode closet., 111, 136-155, 1994.

Salmon, J.K and M.S. Warren, Parallel supercompting with comodity components, Proc. Intl. Conf. Parallel Distributed Processing Tech. Appl. (PDPTA '97), ed. M.S> Warren, D.J. Becker, M.P. Goda, J.K. Salmon and T. Sterling, Las Vegas, NV, June 30-July 3, 1997.

Samet, H. (1990), Design and Analysis of Spatial Data Structures, (Reading, MA: Addison-Wesley), 1990.

Sammis, C.G., D.Sornette and H. Saleur, Complexity and earthquake forecasting, pp. 143-156, in JB Rundle, DL Turcotte, W. Klein, eds., Reduction and Predictability of Natural Disasters, vol. XXV in Santa Fe Institute series in Sciences of Complexity, Addison Wesley, 1996.

Sanders, C.O., Interaction of the San Jacinto and San Andreas fault zones, southern California: Triggered earthquake migration and coupled recurrence intervals, Science, 260, 973-975, 1993.

Savage, J.C., Criticism of some forecasts of the National earthquake Prediction Evaluation Council, Bull. Seismol. Soc. Amer., 81, 862-881, 1991.

Savage, J.C., The Parkfield prediction fallacy, Bull. Seismol. Soc. Amer., 83, 1-6, 1993.

Savage, J.C., W.H. Prescott, and G. Gu, Strain accumulation in southern California, 1973-1984, J. Geophys. Res., 91, 7455-7473, 1986.

SCEC (Southern California earthquake Center, Working group on California earthquake probabilities), Seismic hazards in southern California: Probable earthquakes, 1994 to 2024, Bull. Seism. Soc. Am., 85, 379-439, 1995.

SCEC (Southern California earthquake Center) Annual Report, University of Southern California, Los Angeles, 1997. (also http://www.scec.org/)

Scholz, C.H., A reappraisal of large earthquake scaling, Bull. Seism. Soc. Am., 84, 215-218, 1994.

Scholz, C.H., The Mechanics of earthquakes and Faulting, Cambridge University Press, Cambridge, U.K., 1990.

Schulman, L.S., Techniques and Applications of Path Integration, John Wiley, New York, 1981.

Schwartz, D.P. and K.J. Coppersmith, Fault behavior and characteristic earthquakes: Examples from the Wasatch and San Andreas faults, J. Geophys. Res., 89, 5681-5698, 1984.

Schwartz, S.Y. and L.J. Ruff, Asperity distribution and earthquake occurrence in the southern Kurile Islands arc, Phys. Earth Planet. Int., 49, 54-77, 1987.

Schwartz, S.Y. and L.J. Ruff, The 1968 Tokachi-Oki and the 1969 Kurile Islands earthquakes: Variability in the rupture process, J. Geophys. Res., 90, 8613-8626, 1985.

Schwartz, S.Y., J.W. Dewey and T. Lay, Influence of fault plane heterogeneity on the seismic behavior in the southern Kurile Islands arc, J. Geophys. Res., 94, 5637-5649, 1989.

Senatorski, P., Fault Zone Dynamics Evolution Patterns, Ph.D. Dissertation, Geophysical Institute of the Polish Academy of Sciences (Polska Akademia Nauk, Instytut Geofizyki), Warsaw, 1993.

Shaw, B.E., J.M. Carlson, and J.S. Langer, Patterns of seismic activity preceding large earthquakes, J. Geophys. Res., 97, 479-488, 1992.

Shaw, BE, Frictional weakening and slip complexity on faults, J. Geophys. Res., 100, 18239-18252, 1995.

Shkoller, S. and Minster, J.B., "Chaos in a Burridge-Knopoff Model with state and rate dependent friction law", submitted to Nonlinear Processes in Geophysics, 1996.

Sibson, R.H., Implications of fault-valve behaviour for rupture nucleation and recurrence, Tectonophys. 211, 283-293, 1992.

Simpson, D.W and P.G. Richards, earthquake Prediction, An International Review, Maurice Ewing vol. 4, Amer Geophys. Un., Washington, DC, 1981.

Sieh, K.E. and others, Near field investigations of the Landers earthquake sequence, April to July, 1992, Science, 260, 171-176, 1993.

Sieh, K.E. and R.H. Jahns, Holocene activity of the San Andreas at Wallace Creek, California, Geol. Soc. Bull., 95, 883-896, 1984.

Smale, S., Differentiable dynamical systems, Bull. Amer. Math. Soc., 73, 747-817, 1967.

Smalley, R.F., D.L. Turcotte and S.A. Solla, A renormalization group approach to the stick slip behavior of faults, J. Geophys. Res., 90, 1884-1900, 1985.

Smalley, R.F., J.L. Chatelain, D.L. Turcotte, and R. Prevot, A fractal approach to the clustering of earthquakes: Applications to the seismicity of the New Hebrides, Bull. Seism. Soc. Am., 77, 1368-1381, 1987.

Sornette, D. and J. Virieux, Linking short-timescale deformation to long-timescale tectonics, Nature, 357, 401-404, 1992.

Sornette, D., A. Johansen, A. Arneodo, JF Muzy and H. Saleur, Complex fractal dimensions describe the hierarchical structure of Diffusion-Limited-Aggregation clusters, Phys. Rev. Lett. , 76, 251-254, 1996.

Sornette, D., and C.G. Sammis, Complex critical exponents from renormalization group theory of earthquakes; implications for earthquake predictions, J. Phys.I France, 5, 607-619, 1995.

Stauffer, D. and A. Aharony, Introduction to Percolation Theory, Taylor and Francis, London, 1992.

Stein, R. S., A. A. Barka, and J. H. Dieterich, Progressive earthquake failure on the North Anatolian fault since 1939 by stress triggering, Geophys. J. Int., submitted, 1996.

Stein, R. S., G. C. P. King, and J. Lin, Stress triggering of the 1994 M=6.7 Northridge, California, earthquake by its predecessors, Science, 265, 1432-1435, 1994

Stein, R.S., G.C.P. King and J lin, Changes in failure stress on the southern San Andreas fault system caused by the 1992 magnitude=7.4 Landers earthquake, Science, 258, 1328-1332, 1992.

Steketee, J.A., On Volterra's dislocations in a semi-infinite elastic medium, Can. J. Phys., 36, 192-205, 1958.

Stuart, W., Strain softening prior to two dimensional strike slip earthquakes, J. Geophys. Res., 84, 2153-2160, 1979.

Stuart, W.D. and T.E. Tullis, Fault model for preseismic deformation at Parkfield, California, J. Geophys. Res., 100, 24079-24101, 1995.

Stuart, W.D., Forecast model for recurring large and great earthquakes in southern California, J. Geophys. Res., 91, 13771-13786, 1986.

Stuart, W.D., Instability model for recurring large and great earthquakes in southern California, Pure Appl. Geophys., 122, 793-811, 1985.

Taylor, M.J., G. Zheng, J.R. Rice, W.D. Stuart and R. Dmowska, Cyclic stressing and seismicity at strongly coupled subduction zones, J. Geophys. Res., 101, 8363-8381, 1996.

Tse, S. and J.R. Rice, Crustal earthquake instability in relation to the depth variation of frictional slip properties, J. Geophys. Res., 91, 9452-9472, 1986.

Turcotte, D.L., earthquake prediction, Ann. Rev. Earth Planet. Sci., 19, 181-194, 263-281, 1991.

Turcotte, DL, Fractals and Chaos in Geology and Geophysics, Cambridge, 1992.

Urbach, J.S., R.C. Madison and J.T. Markert, Phys. Rev. Lett., 75, 276 (1995).Vasconcelos, G.L., M. de Sousa Vieira, and S.R. Nagel, Implications of a conservation law for the distribution of earthquake sizes, Phys. Rev. A., 44, R7869-R7872, 1991.

Wald, D.J., D.V. Helmberger, and T.H. Heaton, Rupture model of the 1989 Loma Prieta earthquake from the inversion of strong-motion and broadband teleseismic data, Bull. Seismol. Soc. Amer., 81, 1540-1572, 1991.

Wallace, T.C., A. Velasco, J. Zhang, and T. Lay, A broadband seismological investigation of the 1989 Loma Prieta, California, earthquake; evidence for deep slow slip?, Bull. Seismol. Soc. Amer., 81, 1622-1646, 1991.

Ward, S,N, and S.D.B. Goes, How regularly do earthquakes recur? A synthetic seismicity model for the San Andreas fault, Geophys. Res. Lett., 20, 2131-2134, 1993.

Ward, S.N. and S. Goes, How regularly do earthquakes recur? A synthetic seismicity model for the San Andreas fault, Geophys. Res. Lett., 20, 2131-2134, 1993.

Ward, S.N., An application of synthetic seismicity in earthquake statistics: the Middle America trench, J. Geophys. Res., 97, 6675-6682, 1992.

Ward, S.N., Synthetic earthquake models for long-term prediction, Geotimes, 37, 18-20, 1992.

Warren, M.S. and J. K. Salmon. Computer Physics Communications, A portable parallel particle program, 87, 266-290, 1995.

Warren, M.S. and J.K. Salmon, A Parallel, Portable and Versatile Treecode, Proc. Seventh SIAM Conference on Parallel Processing for Scientific Computing, San Francisco, CA, 15--17 Feb., 1995: 319--324.

Warren, M.S. and Salmon, J.K., Computer Physics Communications, 87, 266-290, 1995.

Warren, MS, P J. Quinn, J.K. Salmon and W H. Zurek, Dark Halos Formed via Dissipationless Collapse: 1. Shapes and Alignment of Angular Momentum, Astrophysical J., 399, 405--425, 1992

Weatherwise, J. Am Met. Sci., June/July, 1995.

Winckelmans, G.S., JK Salmon, MS Warren, A Leonard and B Jodoin, Application of fast parallel and sequential tree codes to computing three-dimensional flows with vortex element and boundary element methods, in Vortex Flows and Related Numerical Methods, Montreal, 1995.

Wuethrich, B., California quake assessed, Trans. Am Geophys. Un. EOS., 75, 41, 1994.

Yeomans, J.M., Statistical Mechanics of Phase Transitions, Clarendon Press, Oxford, 1992.

Zheng, G., Y. Ben-Zion, J.R. Rice and J. Morrissey, A new method for calculating elastodynamic response over long stressing histories containing rapid rupture episodes, Trans. Am. Geophys. Un. EOS (Suppl.), 76, F405, 1995.