Definition of an integer M mod N = the remainder of M/N.

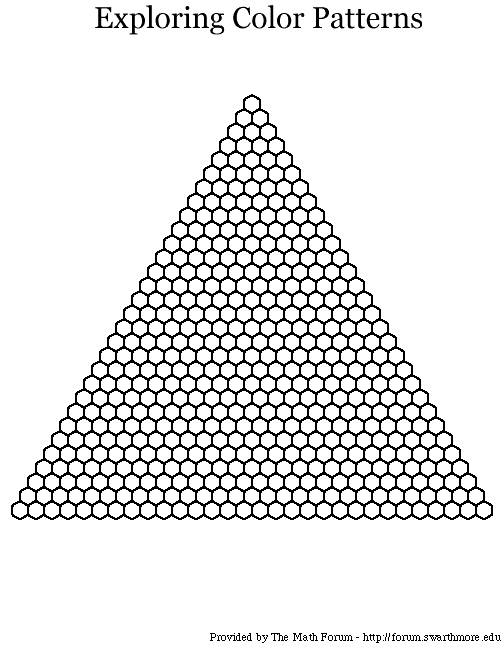
One way of seeing patterns in Pascal's triangle is to color all the numbers M in the triangle such that M mod N is equal to 0 in one color, and all the other numbers in a second color.

• Try this for N = 2. (This pattern is the Sierpinski triangle, which is an example of a fractal.)
• Now try it for N = 3, 5, and 7. Are the patterns similar?
• Note that it is easier to compute the Pascal numbers mod N, if you generate them that way from the top. Use the rule that every interior number in the triangle is the sum of the two numbers above it, except take the answer mod N and put that in for the Pascal number. Continue generating the triangle.

Note that these explorations take a long time to color by hand. What we need is a computer program to draw them for us!