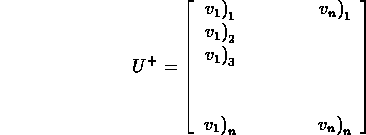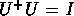Next: Diagonal Form of
Up: No Title
Previous: Orthogonality of Eigenvectors
- We choose to normalize each eigenvector
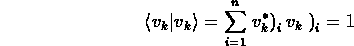
- and we have proved
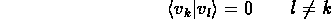
- eigenvectors are ORTHOnormal whether or not eigenvalues are
degenerate
- Define a matrix U so that columns of
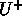 are orthonormal
eigenvectors
are orthonormal
eigenvectors
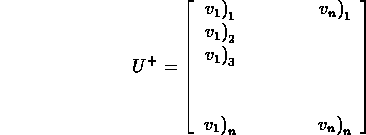
- U is UNITARY
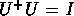
- This unitary condition is exactly the orthonormality condition.
Geoffrey Fox, Northeast Parallel Architectures Center at Syracuse University, gcf@npac.syr.edu
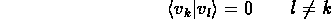
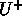 are orthonormal
eigenvectors
are orthonormal
eigenvectors
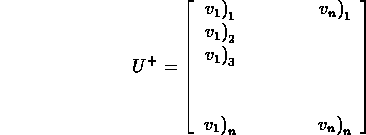
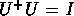
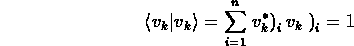
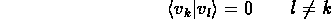
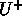 are orthonormal
eigenvectors
are orthonormal
eigenvectors