
where Q is Marquardt's Parameter

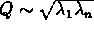 . Then shifts
. Then shifts 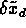 are unchanged for large
are unchanged for large 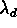 , small for small
, small for small
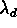 .
.
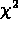 increases when you use (NL.1).
increases when you use (NL.1).
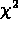 decreases when you use (NL.1).
decreases when you use (NL.1).

where Q is Marquardt's Parameter

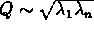 . Then shifts
. Then shifts 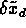 are unchanged for large
are unchanged for large 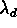 , small for small
, small for small
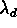 .
.
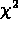 increases when you use (NL.1).
increases when you use (NL.1).
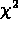 decreases when you use (NL.1).
decreases when you use (NL.1).