The Application Groups at PAWS '96 posed a set of questions to the point design teams that were designed to quantify the differences and relative capabilities of the designs. We received five responses that revealed, as we will see, as much about the questions as the machines! So, we present this section partly as a contribution to a good set of metrics and discriminators for evaluating diverse architectures.
The text presents the original set of questions, which are grouped into eight delineating broad features, and one (question #9 with six parts) with a set of simple kernels for which one is asked to analyze expected performance. We present and analyze the response of:
For clarity, we have sometimes also given scaled numbers in response to a uniform 1 Petaflop peak performance. Below, we make some broad remarks on the review and then follow with specific remarks for each section, going through questions 1, 3, 9, 2, 4--8 in an order that links benchmarks with detailed machine parameters.
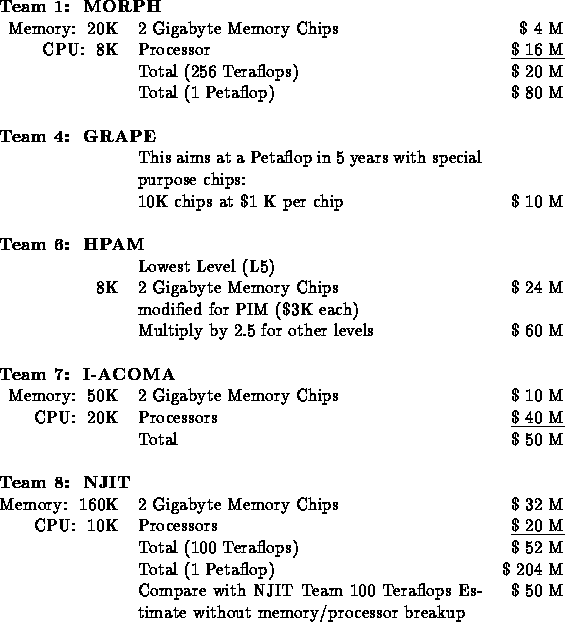
1. Estimated Cost
The question asked --- use the SIA estimate that semiconductor hardware will be 25 times cheaper per transistor in the 2006 time frame than it is in 1996. You may take $50 per Megabyte for 1996 memory and $5 per Megaflops per second for 1996 sustained RISC processor performance (which roughly scales with transistor count), or else otherwise justify your estimate.
General Remarks
It was correctly noted by some responders that $5 per sustained Megaflops per second (quoted in question) was not so easy to use as ``sustained'' depends on application analysis, and easier is processor chip cost. We changed cost estimates to $2,000 a processor chip and $0.1 per Megabytes of memory in 2007. Note: 1994 SIA projections are $80 for a volume microprocessor chip and $0.04 per Megabyte for volume DRAM in the year 2007 (this is $80 per a single two-Gigabytes memory DRAM chip). In the table below, we used this uniform estimate, and not that given by Point Groups who made varied assumptions.
The high cost per processor includes estimates of low volume, packaging and connection costs. The DRAM is assumed to be a little more than SIA volume cost, as used near start of introduction when price will be higher than volume cost. Note that the wide variation of total Petaflop cost recorded below largely reflects different total memory assumptions. This reflects

3. Hardware Specifications
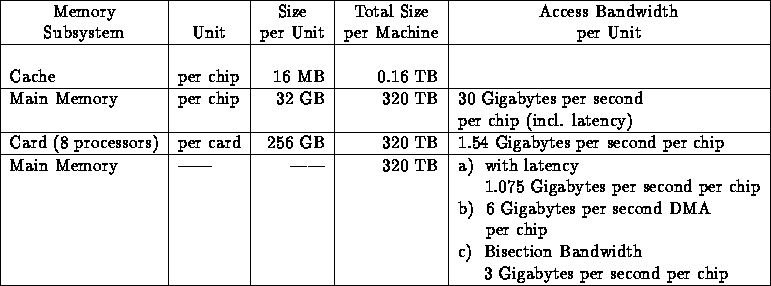
Here the question asked for peak performance rates of processors, sizes and structures of the various levels of the memory hierarchy (including caches), latency and bandwidth of communication links between each level, etc. The answers here were difficult to collate---partly because different architectures are naturally described differently, but partly because we were not very precise in the question. We record first the processor structure, and then the memory hierarchy.
Processors and Their Characteristics
Note that base chip is typically 1 GHz with performance varying from 10 Gigaflops (Team 8) to 64 Gigaflops (Team 7). This represents uncertainty in technology extrapolation for the basic high-performance microprocessor.
Team 1: MORPH (256 Teraflops)
8K, 1 GHz Processor chips each containing four or eight C.P.U.'s with a peak performance of 32 Gigaflops per chip.
Team 4: GRAPE
10K Specialized Processor chips performing at 90 Gigaflops/chip
Team 6: HPAM
This has five levels

Team 7: I-ACOMA
Processor chip is eight C.P.U.'s (or threads), each issuing eight instructions per 1 GHz cycle. Sustained performance of 50 Megaflops, peak 64 Megaflops. 20K processor chips, packaged as 2,000 nodes. Each node is a 10 C.P.U. shared memory system.
Team 8: NJIT (100 Teraflops)
Processor chip is 1 GHz and peak performance is 10 Gigaflops. The base machine has 10,368 processors.
Memory Hierarchy
Here, there is even more variation in design and presentation. One
remarkable architectural differences is the variation in the amount of
memory on chip in the various designs. This varies by a factor of
1,000 from a few Megabytes (Team 7, 8) to
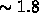 Gigabytes (Team
2, 6). The petakernels seem to favor large chip caches and it would
seem that there may be an optimal design in between these extremes.
Gigabytes (Team
2, 6). The petakernels seem to favor large chip caches and it would
seem that there may be an optimal design in between these extremes.
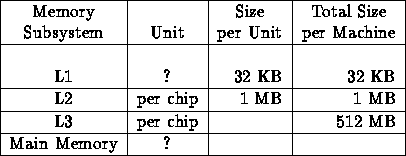
We found answers difficult to interpret unambiguously as the unit was often not clear---was the L1 cache per C.P.U. (of which there are many chips) or per chip!
We have devised a table, and inserted some material in it. This table---as we will see in Question 9---has data of relevance to analyzing performance, and encompasses all information presented by teams. However, no team clearly gave all the information!
The table has, in general, the following columns: memory subsystem, unit of subsystem, size per unit, total size per machine, page or cache line size, latency, and access bandwidth per unit (but we only record in each table for a given team those for which we have data).
Note that the highest level of memory often has two sets of characteristics---one viewed as memory per processor node---another viewed as the total distributed shared memory seen by all (other) nodes.


9. Quantitatively assess the performance of the proposed
system on the following computational problems, based on design
parameters and execution model. Justify the analysis. In the
following, 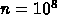 ; arrays are
presumed appropriately dimensioned.
; arrays are
presumed appropriately dimensioned.
do i = 1, n c(i) = 3.141592653589793 * a(i) + b(i) enddo
do i = 1, n b(131*i) = a(131313*i) enddo
! This loop initializes the array idx with pseudo-random numbers ! between 1 and n. do i = 1, n idx(i) = 1 + mod (13131313*i, n) enddo
! Tested loop: do i = 1, n b(idx(i)) = a(i) enddo
nc = 5; nx = 1000; ny = 1000; nz = 1000
do k = 1, nz
do j = 1, ny
do i = 1, nx
do m = 1, nc
do mp = 1, nc
a(i,j,k,m) = u(mp,m) * (b(i+1,j,k,mp) + b(i-1,j,k,mp) &
b(i,j+1,k,mp) + b(i,j-1,k,mp) + b(i,j,k+1,mp) + &
b(i,j,k-1,mp)) + a(i,j,k,m)
enddo
enddo
enddo
enddo
enddo
enddo
nc = 150; nx = 100; ny = 100; nz = 100
Consider a tree structure, such as
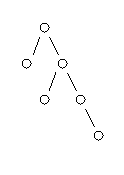
except with 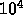 nodes and an arbitrary structure, with
one random integer at each node. Is this tree a subtree of a similar
tree of size
nodes and an arbitrary structure, with
one random integer at each node. Is this tree a subtree of a similar
tree of size 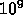 nodes? Find the path to the node of the subtree in
the large tree.
nodes? Find the path to the node of the subtree in
the large tree.
General Comments on Question 9 (Petakernels)
The current kernels are too small as they use such a sufficiently
small amount of memory (Table A) that in many machines, all the data
can be fitted in (one of) the caches. For instance, the vector
applications 9a),b),c) should have a size
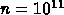 to get to
Terabyte storage level.
to get to
Terabyte storage level.
Further, we need to define initial positioning of data. You get much better performance if you can assume data already in cache (natural if kernels iterated) than if you have to move. Fox suggests taking large kernels (which don't all fit in cache) but calculate performance with optimal positioning of data.
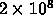 Double Precision
Operations with memory needs of 2.4 Gigabytes. Time at one Petaflop is
Double Precision
Operations with memory needs of 2.4 Gigabytes. Time at one Petaflop is
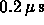 if
if
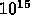 floating operations per second
can be realized.
floating operations per second
can be realized.
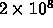 Operations with memory
need of 1.6 Gigabytes.
Natural minimum time at one Petaflops is
Operations with memory
need of 1.6 Gigabytes.
Natural minimum time at one Petaflops is
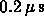 . Of
course, large stride implies that one expects to be dominated by
fetching data, and so will ``see'' the cross-sectional bandwidth, and
not C.P.U. performance.
. Of
course, large stride implies that one expects to be dominated by
fetching data, and so will ``see'' the cross-sectional bandwidth, and
not C.P.U. performance.
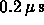 as
``unit''
performance. Note that first loop setting idx was correctly
viewed as initialization by some point groups who only analyzed
performance on second loop.
as
``unit''
performance. Note that first loop setting idx was correctly
viewed as initialization by some point groups who only analyzed
performance on second loop.
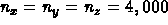 perhaps) and
perhaps) and
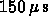 timing (for one
Petaflop) optimal performance.
timing (for one
Petaflop) optimal performance.
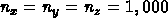 to get a factor of 1,000 more
memory), and has
to get a factor of 1,000 more
memory), and has
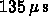 timing for one Petaflop optimal
performance.
Notice that it is most natural to parallelize over
timing for one Petaflop optimal
performance.
Notice that it is most natural to parallelize over
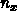 ,
,
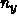 ,
,
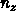 and leave m and mp loops ``inside node'' as these full matrix
operations lead to most data re-use.
and leave m and mp loops ``inside node'' as these full matrix
operations lead to most data re-use.
 operations
to decide that a tree with
operations
to decide that a tree with
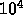 nodes is not contained in one
with
nodes is not contained in one
with 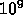 nodes. We need a
parallelism of at least
nodes. We need a
parallelism of at least 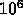 in any
Petaflop machine to achieve maximal performance.
in any
Petaflop machine to achieve maximal performance.
The algorithm needs to specify a little more about the tree to decide on
the best algorithm. If integers at nodes are random, then one needs
only to compare root of small tree with integers at nodes of large
tree to reject a possible match! Suppose big tree was nine levels each
with 10 children for 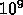 nodes, and
little tree was a similar
four-level branching of 10 data structure. Then we need only to
compare root to nodes at top five levels of big tree. In general,
performance depends on branching factors and how often one will get
matches. ``Random'' integers will match rarely!
nodes, and
little tree was a similar
four-level branching of 10 data structure. Then we need only to
compare root to nodes at top five levels of big tree. In general,
performance depends on branching factors and how often one will get
matches. ``Random'' integers will match rarely!
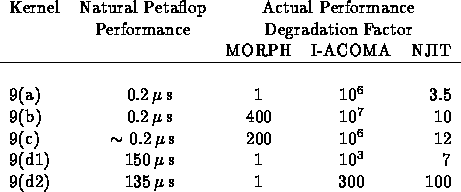
We give, in Table B, a summary of projected performance relative to naive optimum. Note that only three point groups gave a full set of numbers, and we ignored 9(e) as, although a nice test, it needs clarification. The projections of Team 7 were pessimistic, as they had poor cache locality, but noted (without details) that prefetching could improve. Team 8 gave no details on their projections. Note that we represent performance by a factor compared to a naive Petaflops machine, and that we scaled each machine to one Petaflop to get this factor, i.e. we removed differences in peak performances in this table.
Team 1: MORPH Detailed analysis of question 9
 256 TeraOps
256 TeraOps
 Can increase performance by
buying more bisection bandwidth $$
Can increase performance by
buying more bisection bandwidth $$
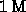 matrix element
matrix element
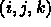
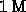 matrix fits in L2 cache,
tile if necessary and prefetch into L1
matrix fits in L2 cache,
tile if necessary and prefetch into L1
What the heck is a good algorithm for this? Can you control the mapping of the tree structure into memory (e.g., cdr-coding?);
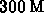 compares/proc (64 bit pointers)
compares/proc (64 bit pointers)
Team 4: GRAPE Detailed analysis of question 9 by Peter Lyster
Quantitative assessment of performance: Prologue---this approach of this team is applicable to cases of loops where there are a large number of operations (say, 1,000) on small numbers of variables (say, 10).
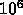 gridpoints these days, and rising not all that rapidly) and large
operational complexity per gridpoint may be amenable to this approach.
For the example that was given, the GRAPE approach may be particularly
useful if
gridpoints these days, and rising not all that rapidly) and large
operational complexity per gridpoint may be amenable to this approach.
For the example that was given, the GRAPE approach may be particularly
useful if 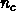 is `large' as computer complexity grows like
is `large' as computer complexity grows like 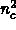 .
.
Attempt (maybe facile) at back-of-the-envelope characterization of Jacobi kernel.
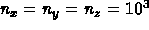 implies
implies 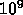 words (gridpoints, cells,
words (gridpoints, cells,
 ). This may be excessive for GRAPE which is now aimed at
). This may be excessive for GRAPE which is now aimed at
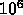 particles, and where cost effectiveness partly comes from small
memory requirements.
particles, and where cost effectiveness partly comes from small
memory requirements.
The inner loops over m and mp have about 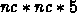 ops. For
nc=5 this gives 125 ops/gridpoint, for
ops. For
nc=5 this gives 125 ops/gridpoint, for  this gives
this gives 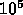 ops/gridpoint. The latter is not dissimilar to the proposed GRAPE
machine parameters.
ops/gridpoint. The latter is not dissimilar to the proposed GRAPE
machine parameters.
For the case 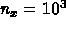 and
and 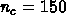 : If the gridpoints are aggregated
in standard domain decomposition for message passing, there are
: If the gridpoints are aggregated
in standard domain decomposition for message passing, there are 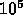 gridpoints per processor, and there are
gridpoints per processor, and there are 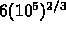 gridpoints
that need to be communicated per `timestep' per processor. Assuming
an interprocessor bandwidth of
gridpoints
that need to be communicated per `timestep' per processor. Assuming
an interprocessor bandwidth of 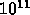 bits per second, and 64 bits
per gridpoint then the communication time is
bits per second, and 64 bits
per gridpoint then the communication time is  seconds. The time to perform the
calculations on chip is approximately
seconds. The time to perform the
calculations on chip is approximately 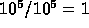 second. So the
ratio of
second. So the
ratio of  and the time per
timestep is one second (not too shabby).
and the time per
timestep is one second (not too shabby).
This methodology is still fairly restricted, notably there are many flops per word, but it may be useful for future applications that require increased speed at fixed resolution. Climate models with modules that couple gridpoint, such as radiation, would present a difficult problem.
Team 6: HPAM Detailed analysis of question 9
The amount of parallelism available in this code is 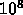 . This
degree exceeds the total number of processors in the HPAM. The
problem would be divided among the different levels, such that the
total execution time is approximately equal.
. This
degree exceeds the total number of processors in the HPAM. The
problem would be divided among the different levels, such that the
total execution time is approximately equal.
The degree of parallelism is  , but the kernel is dominated by
accesses to a vector with large stride; no flops. This kernel would
be executed on one level, the lowest level, for which the memory
latency is less than going between levels.
, but the kernel is dominated by
accesses to a vector with large stride; no flops. This kernel would
be executed on one level, the lowest level, for which the memory
latency is less than going between levels.
The degree of parallelism is 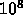 , but the kernel is dominated by
irregular, indirect memory accesses. This kernel would be executed on
one level, the lowest level. No flops.
, but the kernel is dominated by
irregular, indirect memory accesses. This kernel would be executed on
one level, the lowest level. No flops.
Reorder the loops to change the dependency structure and assign the innermost loops to the processors at the lower level.
Divide the 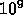 node tree into subtrees with
node tree into subtrees with 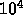 nodes subtrees
and distributed these subtrees among the processors and each processor
perform a comparison to see if the original
nodes subtrees
and distributed these subtrees among the processors and each processor
perform a comparison to see if the original 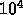 tree is a subtree
of the partitioned tree.
tree is a subtree
of the partitioned tree.
Performance of Kernels for the HPAM Architecture
The answers to the performance of some of the kernels for the HPAM Petaflop Point Design are given for two different conditions:
Case A: the entire HPAM machine is dedicated to the kernel
Case B: the kernel is a part of a large application for which other parts of the application are being executed simultaneously with the kernel; for this case we identify the best level for the kernel (assuming it will be executed on only one level) and describe the performance.
For all cases,  and arrays are presumed appropriately
dimensioned.
and arrays are presumed appropriately
dimensioned.
do i = 1, n c(i) = 3.141592653589793 * a(i) + b(i) enddoIt is assumed that the COTS will have extended double precision representation of floating point numbers, allowing for 128-bit floating point numbers. The value of pi would be represented by a 128-bit number and computations would be executed using this format to maintain the accuracy.
Case A: The amount of parallelism available in this code is 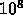 .
This degree exceeds the total number of processors in HPAM. The
problem would be divided among the different levels, such that the
execution time of each level is approximately equal; the load assigned
to each level would be inversely proportional to the speed of the
processors used in the different levels.
.
This degree exceeds the total number of processors in HPAM. The
problem would be divided among the different levels, such that the
execution time of each level is approximately equal; the load assigned
to each level would be inversely proportional to the speed of the
processors used in the different levels.
Case B: Because of the high degree of parallelism and the regularity of memory accesses, the lowest level (bottom level) of HPAM is best for this kernel.
do i = 1, n b(131*i) = a(131313 * i) enddo
do i = 1, n tempb(i) = a(131313 * i) enddo
do i = 1, n
b(131 * i) = tempb(i)
enddo
This problem is memory bound, requiring only memory accesses with a
large stride; no floating point operations are used. The memory
access pattern is such that there is no temporal or spatial locality.
Each reference to the arrays will incur a cache miss. The approach to
efficiently executing this problem involves a combination of code
transformation, prefetching and post-storing. Given the large stride
of the accesses, it would be best to execute the kernel on one of
levels that has the required memory. The level of choice would have
memory access times and parallelism degree (i.e., number of
processors) that yield the best execution time. Execution on only one
level avoids the high cost of intralevel communication versus
interlevel communication.
Further, the elements of ``a'' would be prefetched as early as possible; the results would be stored in ``b'' as late as possible to allow access of ``a''.
do i = 1, n idx(i) = 1 + mod(13131313 * i, n) enddo
do i = 1, n b(idx(i)) = a(i)This problem is very similar to the previous problem, but now the array accesses are indirect and irregular. Again prefetching would be used. The array ``idx'' would be accessed ahead of the array ``b''; the array ``b'' would be accessed ahead of array ``a''. The array ``a'' has a very regular access, exhibiting spatial locality.
Also, given the irregular large stride and irregular access of ``b'', it would be best to execute the kernel on one of the levels that has the required memory. The level of choice would have memory access times and parallelism degree (i.e., number of processors) that yield the best execution time.
do i = 1, nz
do j = 1, ny
do k = 1, nx
do m = 1, nc
do mp = 1, nc
a(i,j,k,m) = u(mp,m) * (b(i+1,j,k,mp) + b(i-1,j,k,mp)
+ b(i,j+1,k,mp) + b(i,j-1,k,mp) + b(i,j,k+1,mp) +
b(i,j,k-1,mp)) + a(i,j,k,m)
enddo
enddo
enddo
enddo
enddo
enddo
The above kernel represents a jacobi kernel for a 3-D grid problem,
where each node corresponds to a supernode with 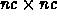 regular
nodes. The computation involves a reduction to accumulate the results
into the array ``a''. The reduction takes place for the ``m'' loop
and is accumulated over the ``mp'' loop.
regular
nodes. The computation involves a reduction to accumulate the results
into the array ``a''. The reduction takes place for the ``m'' loop
and is accumulated over the ``mp'' loop.
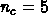 ,
, 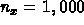 ,
, 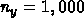 ,
, 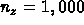
For this case, since  is small,
the m and mp loops can be
mapped to a single processor. The i, j, and k loops
can be mapped to different processors. The combination of these three loops
results in a parallelism of
is small,
the m and mp loops can be
mapped to a single processor. The i, j, and k loops
can be mapped to different processors. The combination of these three loops
results in a parallelism of 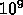 .
.
Case A: The i, j, and k loops can be distributed among all the processors in the HPAM machine, such that the execution time of each level is approximately equal. The load assigned to a processor would be inversely proportional to the processor speed. Each processor would execute the reduction for a given value of i, j, and k. It is assumed that the processors have the appropriate values of b. The array u is small enough so that it can be replicated in all the processors.
Case B: Given the high degree of parallelism of the three loops and the fact that no interlevel communication is needed for the reduction for a specified i, j, and k, these three loops can be distributed over the lowest level of HPAM.
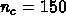 ,
, 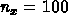 ,
,  ,
, 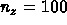
Now the core of the m and mp loops would be executed a total of
22,500 times with some dependencies in the reduction. This is three
orders of magnitude larger than the previous case. The combination of
the i, j, and k loops has a degree of parallelism of 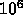 .
.
Case A: Again the i, j, and k loops can be distributed across the entire machine with one major difference. The m and mp loops can be distributed across a group of processors within the same level. The processors within a group would have the same i, j, and k values, but different values of m and mp. In this way, the reduce operation would occur over a small number of processors within the same level, thereby avoiding excessive interlevel communication.
Case B: The kernel would be executed on the lowest level because of
the 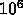 degree of parallelism for the i, j, and k loops. The
m and mp loops would be distributed over a group of processors,
similar to Case A, but all the processors are now in the lowest level.
degree of parallelism for the i, j, and k loops. The
m and mp loops would be distributed over a group of processors,
similar to Case A, but all the processors are now in the lowest level.
Problem: Is there a subtree of size 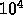 nodes within a similar
tree of size
nodes within a similar
tree of size 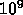 nodes.
nodes.
The solution method would depend on the algorithm chosen for this
problem. A perhaps naive approach is as follows: First construct all
possible distinct (not necessarily disjoint) subtrees with 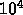 nodes of the original tree. Next, test whether each tree matches the
desired subtree. Explicitly generating and storing each subtree would
be extremely memory intensive, but certainly possible if memory was
available. Alternatively, assuming the original tree is decomposed
into distinct disjoint subtrees, all subtrees that overlap with one of
these subtrees can be generated within a topological neighborhood of a
given subtree and processor assigned to it. Distribute these subtrees
among the processors (one or more per processor depending on the
relative speed of the processors). Let each processor perform a
comparison to see if the desired
nodes of the original tree. Next, test whether each tree matches the
desired subtree. Explicitly generating and storing each subtree would
be extremely memory intensive, but certainly possible if memory was
available. Alternatively, assuming the original tree is decomposed
into distinct disjoint subtrees, all subtrees that overlap with one of
these subtrees can be generated within a topological neighborhood of a
given subtree and processor assigned to it. Distribute these subtrees
among the processors (one or more per processor depending on the
relative speed of the processors). Let each processor perform a
comparison to see if the desired  subtree is a subtree of the
subtree(s) in the processor or those subtrees that result from adding
nodes from neighbor processors (this would require an algorithm).
This can be distributed across the entire HPAM machine. Interlevel
and intralevel communication would be required between processors with
adjacent edges of the tree. This communication would hopefully be
infrequent relative to the computational requirements of the local
tree comparison.
subtree is a subtree of the
subtree(s) in the processor or those subtrees that result from adding
nodes from neighbor processors (this would require an algorithm).
This can be distributed across the entire HPAM machine. Interlevel
and intralevel communication would be required between processors with
adjacent edges of the tree. This communication would hopefully be
infrequent relative to the computational requirements of the local
tree comparison.
An alternative method is to represent the tree as a two-dimensional
sparse matrix, such that 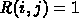 if j is a child of i and 0
otherwise. Then, pattern matching for the sparse matrices would be
used.
if j is a child of i and 0
otherwise. Then, pattern matching for the sparse matrices would be
used.
Team 7: I-ACOMA Detailed analysis of question 9
Single precision. The operations will be performed within a cluster, assuming the data is in memory (150 cycles to get it). Processors cycle at 1 GHz (1 ns cycle time). Loop is fully parallel, so each of the 10 processors does 1/10th of the operations. For simplicity, assume that the stores are non-blocking, therefore, complete in the background. Assume that the loads are blocking (only one load per processor at a time). Assume that there is no prefetching of data. Assume that, compared to cache misses, the mpy and add operations take negligible time. Cache lines are 64 bytes long.
So, each processor needs to read 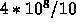 bytes of a() and
bytes of a() and 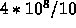 bytes of b(). That is
bytes of b(). That is 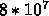 . Every 64 bytes,
there is a miss. This is then
. Every 64 bytes,
there is a miss. This is then 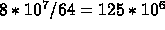 misses. Each miss costs 150 ns so:
misses. Each miss costs 150 ns so: 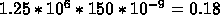 seconds.
seconds.
Note that with prefetching, this number can be reduced considerably.
Similar case as above, except that every single load misses. There
are 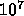 loads per processor, each taking 150 ns. The total time is
then
loads per processor, each taking 150 ns. The total time is
then 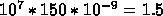 seconds.
seconds.
Takes the same amount of time than a) because we are reading two arrays: a() and idx() sequentially. The store (which stores in b() in a random manner) does not take time in our assumptions. Total time = 0.18 seconds.
First, we reorganize the loop nest as follows:
do k
do m
do mp
do j
do i
and we parallelize the k and m loops. There are 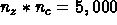 tasks that can be executed in parallel. We give one to each
processor. Each processor then executes the loop nest:
tasks that can be executed in parallel. We give one to each
processor. Each processor then executes the loop nest:
do mp
do j
do i
for a given value of  .
.
As usual, time is determined by the misses. The misses in array u() are negligible. Let us consider the misses in b() and a().
For a():
A processor reads the plane  which is
which is 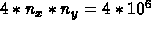 contiguous bytes. This is reused
contiguous bytes. This is reused 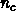 times thanks to loop
do mp. Suppose that we block it so that it fits in the primary
cache. Then, we only need to bring the data once. As usual, every 64
bytes there is a miss. Each miss is serviced in 150 ns. So, total
time is
times thanks to loop
do mp. Suppose that we block it so that it fits in the primary
cache. Then, we only need to bring the data once. As usual, every 64
bytes there is a miss. Each miss is serviced in 150 ns. So, total
time is 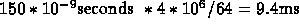 .
.
For b():
A processor reads three planes: 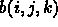 ,
, 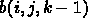 , and
, and
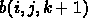 , for a given value of mp. This is
, for a given value of mp. This is 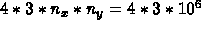 contiguous bytes. However, it will read
contiguous bytes. However, it will read
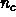 different such three-plane chunks. So, the total data will be
different such three-plane chunks. So, the total data will be 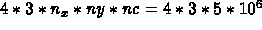 . We will
again block, and every 64 bytes suffer a miss. So, total time is
. We will
again block, and every 64 bytes suffer a miss. So, total time is 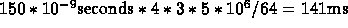 .
.
So, the total Jacobi for the large problem size without prefetching
takes 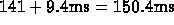 .
.
For the small problem size, the time is
For a(): 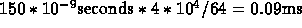
For b(): 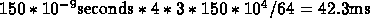 .
.
Total time = 42.39 ms
This is a complex algorithm that can take a variable amount of time. We offer just some intuition here.
We need to compare a tree with 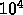 elements to one with
elements to one with 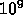 elements. Assume that each element is 12 bytes: a leftpointer, the
integer, and the right pointer. We can partition the
elements. Assume that each element is 12 bytes: a leftpointer, the
integer, and the right pointer. We can partition the 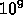 tree
among the 2,000 nodes (it fits in memory):
tree
among the 2,000 nodes (it fits in memory): 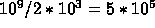 elements per node. Then, each of the 10 processors in a node
works on 1/10 of the elements; that is each processor works on
elements per node. Then, each of the 10 processors in a node
works on 1/10 of the elements; that is each processor works on 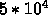 elements of the large tree.
elements of the large tree.
Each processor will therefore read:
Small tree: 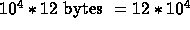 contiguous
bytes. One miss every 64 bytes means we have 1,875 misses
(negligible).
contiguous
bytes. One miss every 64 bytes means we have 1,875 misses
(negligible).
Fraction of the large tree:  elements. Suppose that the
data are not contiguous. We will suffer
elements. Suppose that the
data are not contiguous. We will suffer 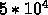 misses (one per
element) which cost 7.5 ms.
misses (one per
element) which cost 7.5 ms.
Assume that all the time is taken by the loading of the data; the operations of the comparison may be assumed free. Then, this first pass of comparisons will cost 7.5 ms.
If none of the processors produces a partial match or one of the processors finds the whole tree, the program finishes. If not, we have to have the processors that produced the partial matches work on their neighbor's chunk of the large tree to finalize the match or prove it wrong. That would be another 7.5 ms. However, the data may now be remote, not local in the cluster. Since a remote miss is at least one order of magnitude more expensive, the operation would take 75 ms.
Overall: the total time is then 82.5 ms.
Team 8: NJIT Detailed analysis of question 9
Execution times: (This is only information they gave!)
2. Programming and Execution Models; Programming Languages
Team 1: MORPH Programming
Team 4: GRAPE Programming
There are driver programs that call specialized functions. The specialized functions are implemented in hardware, while the drivers are written in F77/C/C++. There exit programmable hardwares that handle a range of different force laws.
Team 6: HPAM Programming
Model: All levels appear as shared memory, but each level can be either message passing or shared memory. The programming of each level can be explicit to the user.
Languages: Fortran (as supported by POLARIS), but there could be others.
Team 7: I-ACOMA Programming
This is a pure shared memory with the hierarchy invisible to the programmer. Prefetching could be allowed, making some aspects visible.
Team 8: NJIT Programming
The user is presented a fully-connected system. Execution model: Two-dimensional MIMD generalized hypercube with 10,368 processors (or 12,800 processors for a fault-tolerant system with I/O capabilities). This generalized hypercube is a two-dimensional system where the processors in each of the two dimensions are fully connected.
4. Synchronization mechanisms; hardware fault tolerance facilities
Team 1: MORPH Synchronization
Team 4: GRAPE Synchronization
The algorithm are self synchronizing through the drive modules. No opinion regarding fault tolerance facilities.
Team 6: HPAM Synchronization
Synchronization: Locks and barriers within levels and between levels. Software based approach and/or backbone approach (including bypasses) in addition to communication backbone.
Fault tolerance: Fall back on different levels; harder to handle within a level.
Team 7: I-ACOMA Synchronization
Support for basic atomic read-modify-write to variables. This support will be used by the libraries to implement locks and barriers, for example.
Team 8: NJIT Synchronization
Up to 2,432 additional processors for fault tolerance (no performance degradation due to ``reconfiguration'').
5. Mass Storage, I/O and Visualization Facilities
Team 1: MORPH I/O
Team 4: GRAPE I/O
There are typically 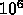 particles, the algorithm performs
particles, the algorithm performs
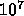 operations/particle/timestep, on average there are a total of
operations/particle/timestep, on average there are a total of
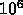 timesteps. Clearly, the memory and I/O to flop ratio is
pretty small.
timesteps. Clearly, the memory and I/O to flop ratio is
pretty small.
Team 6: HPAM I/O
Mass Storage: Network connection between levels
I/O: Multiple I/O co-processors
Team 7: I-ACOMA I/O
Distributed I/O: One or more disks per node. All I/O is shared.
Team 8: NJIT I/O
All three features are implemented in our system.
6. Support for extended precision (i.e., 128-bit and/or higher precision integer and floating-point arithmetic)---hardware or software.
Team 1: MORPH Precision
This support could be added if necessary.
Team 4: GRAPE Precision
The core operations are 32 bit. Some operations that need higher accuracy are 64 bit. The latter (64 bit) and may need to be extended to 128 bit. Presumably, this is just a matter of changing the specifications to the chip maker.
Team 6: HPAM Precision
Team 8: NJIT Precision
128-bit floating-point arithmetic
7. Which of the 10 key federal grand challenge applications will the proposed system address (aeronautical design, climate modeling, weather forecasting, electromagnetic cross-sections, nuclear stockpile stewardship, astrophysical modeling, drug design, material science, cryptology, molecular biology).
Team 1: MORPH Applications
Federal Grand Challenge Programs (drug design, molecular biology, astrophysical modeling) + interactive 3D visualization
Team 4: GRAPE Applications
Astrophysical modeling. To the extent that plasma physics problems (using particles) may be addressable, then include materials science and nuclear fusion. The question of wider applicability doesn't appear to have been addressed by the team (see also comments in prologue to Section 9 for this team) and this may be a fruitful area to investigate, notably climate modeling, see item 9d for this team.
Team 6: HPAM Applications
Architecture mapping to federal grand challenges was a general purpose machine with target applications for validation: aeronautical design (CFD, FEM), astrophysical, and molecular biology
Team 7: I-ACOMA Applications
Can handle all types of applications easily because it is a general-purpose shared-memory machine. Specially easy to program for irregular applications and applications with fine-grain sharing.
Has hardware support for sparse computations and databases.
Sparse type computations: Because they are difficult to parallelize. Databases: Because they are very important. For both types of applications, we have special hardware support.
Team 8: NJIT Applications
Climate modeling and weather forecasting
8. Reliance on novel hardware and/or software technology, to be developed by the commercial sector.
Team 1: MORPH Custom Technology
No novel requirements of the commercial sector, we will develop technology for hardware synthesis appropriate for customization of cache and network management, as well as hardware performance monitoring.
Team 4: GRAPE Custom Technology
This uses custom chip designs, but rather conservative technology. For applications where this approach is appropriate (i.e., where a lot of operations are performed on not a lot of memory) the chips need to be designed by scientist/engineers, however they don't cost a lot to manufacture, or stress fabrication methodology.
Team 6: HPAM Custom Technology
Hardware: PIM, Optical Interconnects
Software: Identification of different degrees of parallelism in program
Team 7: I-ACOMA Custom Technology
The system only needs to have extra support in the processor chip (to support multithreading, COMA, and the hardware for sparse computations).
It is not too revolutionary. Assumes natural progress in
Team 8: NJIT Custom Technology
Our design could benefit from improvements in current technology. Its success, however, does not really depend on any hardware innovations. Improved compiler technologies, better programming languages, and performance visualization strategies could enhance usability; this is true for any system designed for near Petaflops performance.