6.5.3 通用(图)构造子 |
MPI_GRAPH_CREATE(comm_old, nnodes, index, edges, reorder, comm_graph)
IN comm_old 不带拓扑的输入通信子(句柄)
IN nnodes 图中节点数(整数)
IN index 整数矩阵描述节点度数(见下)
IN edges 整数矩阵描述图边数(见下)
IN reorder 标识数可以从排序(true)或不能(false)(logical)
OUT comm_graph 带有所加的图拓扑的通信子(句柄)
int MPI_Graph_create(MPI_Comm comm_old, int nnodes, int *index, int *edges,
int reorder, MPI_Comm *comm_graph)
MPI_GRAPH_CREATE(COMM_OLD, NNODES, INDEX, EDGES, REORDER, COMM_GRAPH, IERROR)
INTEGER COMM_OLD, NNODES, INDEX(*), EDGES(*), COMM_GRAPH, IERROR
LOGICAL REORDER
MPI_CART_CREATE返回一个指向新的通信子的句柄, 这个句柄与笛卡尔拓扑信息相联系。如果reorder = false, 那么在新组中每一进程的标识数就与在旧组中的标识数相一致。否则, 函数会重新对进程编号。如果图的大小, nnodes,小于comm组的大小, 那么有些进程返回MPI_COMM_NULL, 类似MPI_COMM_CREATE。如果说明的网格大于组的尺寸, 调用出错。
三个参数nnodes、index和edges定义了图的结构。nnodes 是图的结点数。结点编号从0到nnodes-1。数组第i号单元的index 存储了前i个图结点的邻居的总数。结点0、1、…、nnodes-1的邻居的列表被存储在数组edges连续的位置中。数组edges表示为一个展开的边列表。index中的单元总数是nnodes,并且edges中的单元总数等于图边的总数。
参数nnodes, INDES和edges的定义以下面的简单的例子说明。
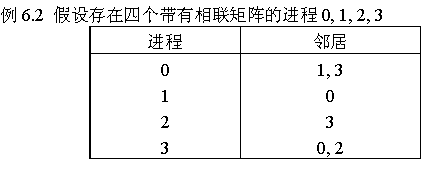
那么, 输入参数为:
nnodes = 4
index = 2, 3, 4, 6
edges = 1, 3, 0, 3, 0, 2
因此, 在C语言中, index[0]是节点0的度数, index[i] - index[i-1] 是节点 i的度数, i=1, ..., nnodes-1; 节点0的邻居列表存储在edges[j]中, 其中0≤j ≤index[0]-1, 节点i的邻居列表, i > 0, 存储在edges[j]中, 其中0≤j ≤index[i]-1。
在Fortran语言中, index(1)是节点0的度数, 并且index(i+1) - index(i)是节点i的度数, i=1, ..., nnodes-1; 节点0的邻居列表存储在edges(j)中, 其中0≤j ≤index(0)-1, 节点i的邻居列表, i > 0, 存储在edges(j)中, 其中0≤j ≤index(i)-1。
对实现者的建议: 下面的拓扑信息很可能与通信子一起存储:
这是定义图结构的向量
对于图结构,结点数等于组中进程数。因此, 没有明显地存储结点数。在数组起始位置上的一个附加的零单元简化了对拓扑信息的访问。(对实现者建议的结束)
| Copyright: NPACT |