The HPJava Project

A Simple Example - Matrix multiplication

Here is an example of an HPJava program for multiplying together two matrices, implemented as distributed arrays:

  Procs2 p = new Procs2(P, P) ;
  on(p) {
    Range x = new BlockRange(N, p.dim(0)) ;
    Range y = new BlockRange(N, p.dim(1)) ;

    float [[,]]  c = new float [[x, y]] ;

    float [[,*]] a = new float [[x, N]] ;
    float [[*,]] b = new float [[N, y]] ;

    ... initialize `a', `b'

    overall(i = x)
      overall(j = y) {

        float sum = 0 ;
        for(int k = 0 ; k < N ; k++)
          sum += a [i, k] * b [k, j] ;

        c [i, j] = sum ;
      }
  }

Distributed arrays a, b and c are declared through special syntax, using double brackets. This distinguishes them from the sequential arrays of ordinary Java. HPJava is a superset of ordinary Java, so ordinary Java arrays are also available in HPJava. But there are several important differences between standard Java arrays and the distributed arrays conventionally used in data-parallel programming. Rather than try to force two incompatible models of an array into the same mold, HPJava lives with the distinction. It keeps the idea of a distributed array strictly separate from the standard Java idea of a sequential array.

Whereas all the elements of an ordinary Java array reside in the memory of the process that creates the array, the elements of a distributed array are divided across the memories of the processes that collectively create the array. Distributed arrays may be multidimensional. In general their shape and distribution is specified in the constructor using a list of distributed range objects. These belong to the class Range. The 2-dimensional array c has ranges x and y. Other languages (including Ada) provide special syntax for describing ranges of integers, to be used in declaring arrays and parametrizing for loops. HPJava elevates its range entities to full object status, and endows them with a distribution format. The range x represents a mapping of the integer interval 0 ... N - 1 into the first dimension of the process grid p (represented by the expression p.dim(0)). The range y is similar, but the interval is distributed over the second dimension of p. The choice of subclass BlockRange for these ranges implies that the intervals are distributed over the process grid dimensions using simple block distribution format. More complex distributions formats are supported through different subclasses of Range. In general a multidimensional array can have ranges with an arbitrary mix of these distribution formats.

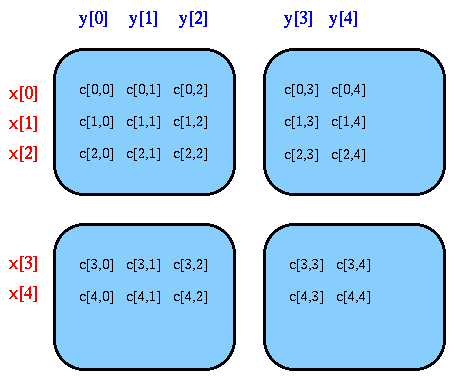
The figure shows the distribution of the elements of c over the 4 processors of p if P = 2 and N = 5.

The arrays a and b are the same shape as c -- they are N by N matrices -- but there distribution patterns are different. The second dimension of a and the first dimension of b are sequential, or collapsed, dimensions. (Actually a sequential array dimension is just a dimension parametrized by a particular subclass of Range called CollapsedRange, but this is a sufficiently simple and important case to warrant special treatment by the compiler.) The type signature of an array with a sequential dimension includes an asterisk in the associated slot, and a simple integer extent is used in the corresponding slot of the constructor. The layout of the elements of a looks like:

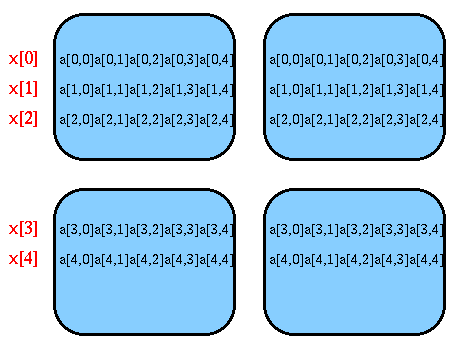
The first dimension of a is distributed over the ``vertical'' process dimension. But because the second dimension of a is sequential every processor contains complete rows of the matrix. Notice that each column of processes contains a replica of the whole array. Because a has no dimension distributed over the second dimension of p, the whole array is replicated across that process dimension.

The distribution of b is complimentary:

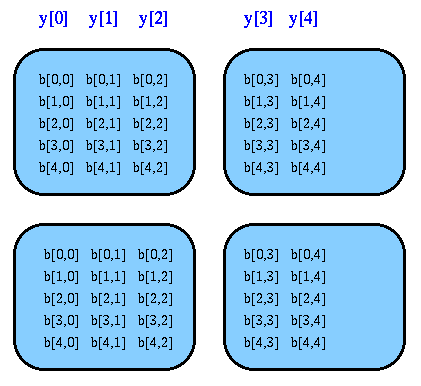
Processes contain whole columns of the matrix, and every row of processes contains a replica of the complete array. The code that initializes a and b should respect this replication pattern, and enter identical values in each copy of the elements of the arrays. In a later section we will illustrate how this requirement may be met.

Because we have carefully selected the distribution patterns for the matrices, the parallel implementation of the matrix multiplication is very straightforward. All the operands for the computation of c[0,0], say, are resident on the processor that holds that element, so no communication is needed to compute that element (or any other element).

The overall construct is a loop parametrized by a range object. Because a Range generally represents a distributed range of integers, an overall is generally a parallel, distributed loop. In the specific example illustrated above the body of the construct

 
    overall(i = x) {
      ...
    }

The implementation of the matrix multiplication should now be reasonably transparent. A pair of nested parallel loops iterate over the elements of c. An inner sequential loop accumulates the inner product of the relevant row of a with the relevant column of b. Notice that, because the second dimension of a and the first dimension of b were explicitly declared to be sequential, the compiler allows them to be subscripted unrestrictedly with integer expressions. The variable sum is simply a local scalar variable.

Next: Process groups