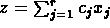 where
where 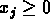 and there are
Linear Constraints
and there are
Linear Constraints
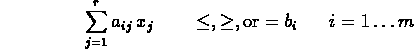
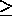 . Write i=1 constraint as
. Write i=1 constraint as
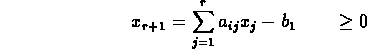

 Minimize
Minimize 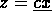
 Subject to
Subject to 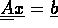 as well as that all components of
as well as that all components of 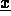 are
positive.
are
positive.
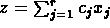 where
where 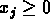 and there are
Linear Constraints
and there are
Linear Constraints
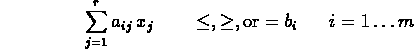
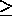 . Write i=1 constraint as
. Write i=1 constraint as
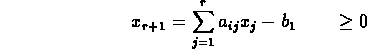

 Minimize
Minimize 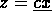
 Subject to
Subject to 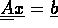 as well as that all components of
as well as that all components of 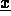 are
positive.
are
positive.