Consider a variable point X in space Y where Y is some subset of
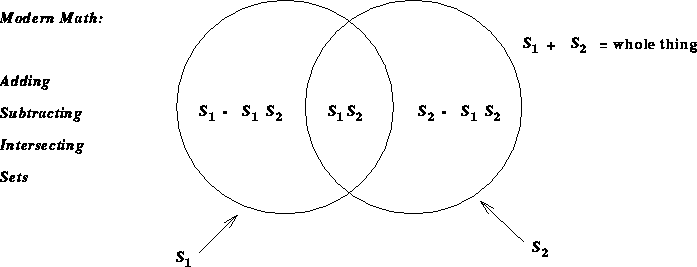
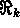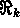( is the k dimensional real Euclidean space).
Further, consider the family of all Borel sets S in Y.
You will, of course, recall that a Borel set is gotten by
performing (finite or denumerably many times) on intervals ,
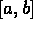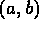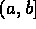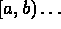, , the operations of addition,
subtraction or multiplication (and continuing process denumerably
often).
(
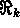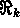is the k dimensional real Euclidean space).
,
, 
, 
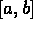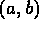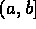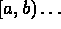the operations of addition,
subtraction or multiplication (and continuing process denumerably
often).
