


Next: Particle Cluster Production
Up: 2: Feefoefum in
Previous: Compound Poisson Distribution
- Particularly interesting is sensitivity to assumption of which
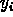 are chosen to be Poisson.
are chosen to be Poisson.
- Note the Poisson distribution with mean (number of
objects)
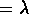 , and where each object counts four units
(telephone calls, etc.), is much broader than ordinary Poisson of mean
, and where each object counts four units
(telephone calls, etc.), is much broader than ordinary Poisson of mean
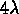 , where each object gives a single unit.
, where each object gives a single unit.
- This is of importance in particle physics where
- We believe that
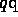 ``clusters'' are produced
independently in a high energy collision.
``clusters'' are produced
independently in a high energy collision.
- These clusters are (assumed to be) Poissonly distributed and
decay into
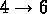 final particles.
final particles.
- One can show that if particles were produced in a Poisson
fashion singly, then
-
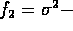 mean for final particles is zero.
mean for final particles is zero.
- However, in cluster model where one can assume
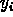 are
distributed Gaussianly with the
are
distributed Gaussianly with the  mean.
mean. 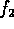 is
always >0.
is
always >0.
- Experimentally, one finds
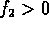 except when perturbed by
kinematic constraints.
except when perturbed by
kinematic constraints.
- i.e., cluster model and experiment is broader than naive
Poisson.
Geoffrey Fox, Northeast Parallel Architectures Center at Syracuse University, gcf@npac.syr.edu
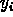 are chosen to be Poisson.
are chosen to be Poisson.
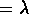 , and where each object counts four units
(telephone calls, etc.), is much broader than ordinary Poisson of mean
, and where each object counts four units
(telephone calls, etc.), is much broader than ordinary Poisson of mean
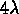 , where each object gives a single unit.
, where each object gives a single unit.
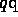 ``clusters'' are produced
independently in a high energy collision.
``clusters'' are produced
independently in a high energy collision.
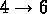 final particles.
final particles.
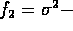 mean for final particles is zero.
mean for final particles is zero.
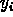 are
distributed Gaussianly with the
are
distributed Gaussianly with the  mean.
mean. 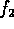 is
always >0.
is
always >0.
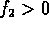 except when perturbed by
kinematic constraints.
except when perturbed by
kinematic constraints.