


Next: Gaussian Limit of
Up: 2: Feefoefum in
Previous: Additivity Property of
- Matthews and Walker confused me by discussing two limits
of binomial distribution.
- We have already discussed one of these---the Poisson
limit---which is really a distinctive limit. However, we can also see
a Gaussian limit which is just a special case of central limit
theorem.
- Although this limit has a particular interpretation because of
the additivity property we just discussed.
- Note also that central limit theorem was discovered in general in
1812 while de Moivre discovered its binomial special case in 1733.
- Let
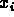 be independent random variables---each of which has the
same
be independent random variables---each of which has the
same 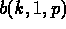 distribution,
distribution,
- i.e., for each
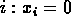 is failure and
is failure and 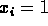 is success with
relative probabilities 1-p and p respectively.
is success with
relative probabilities 1-p and p respectively.
- Then
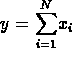 is in fact, k, the
number of successes in n Bernoulli trials.
is in fact, k, the
number of successes in n Bernoulli trials.
Geoffrey Fox, Northeast Parallel Architectures Center at Syracuse University, gcf@npac.syr.edu
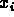 be independent random variables---each of which has the
same
be independent random variables---each of which has the
same 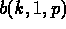 distribution,
distribution,
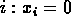 is failure and
is failure and 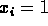 is success with
relative probabilities 1-p and p respectively.
is success with
relative probabilities 1-p and p respectively.
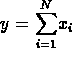 is in fact, k, the
number of successes in n Bernoulli trials.
is in fact, k, the
number of successes in n Bernoulli trials.
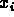 be independent random variables---each of which has the
same
be independent random variables---each of which has the
same 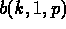 distribution,
distribution,
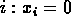 is failure and
is failure and 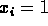 is success with
relative probabilities 1-p and p respectively.
is success with
relative probabilities 1-p and p respectively.
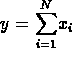 is in fact, k, the
number of successes in n Bernoulli trials.
is in fact, k, the
number of successes in n Bernoulli trials.