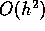Derivative routines, Vertex Centered

Spatial derivative routines contain routines for Inner boundary, Outer boundary and interior. Time derivatives, 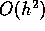use a 3 level leap frog scheme. All derivative routines are second order for the first derivative in x,y,z directions.

To handle the hole, 2 non-distributed lists are created, m(nl),d(nl) where m(l) contains the i,j,k location of the ``hole'' points and d(l) contains either (1,-1,0) indicating either forward, backwards or centered.

The derivatives around the hole are determined to second order. Second derivatives, for example 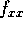, are only first order accurate, although the interior points for the second derivatives are second order accurate (the boundaries are first order accurate). The routine looks as follows:

      subroutine diff(h,f,df,dir,m,d,nl)
      use params
      implicit none
      real*8 h
      real*8, dimension(nx,ny,nz) :: f,df
      real*8, dimension(3*nl)     :: d
      integer, dimension(3*nl)    :: m
      character dir
!HPF$ PROCESSORS PROC(nproc)
!HPF$ DISTRIBUTE f *(BLOCK,*,*) ONTO *PROC
!HPF$ ALIGN(:,:,:) WITH *f(:,:,:)         :: df
      call diff_int(h,f,df,dir)
      call diff_ob(h,f,df,dir)
      if (nl.gt.1) call diff_ib(h,f,df,dir,m,d,nl)
      return
      end

      subroutine diffx_ib(h,f,df,m,d,nl)
      use params
      implicit none
      integer nl
      real*8, dimension(nx,ny,nz) :: f,df
      real*8, dimension(3*nl)     :: d
      integer, dimension(3*nl)    :: m
      real*8 h,h2
      integer i,j,k,l

      h2 = 0.5d0 / h

      do l = 1 , nl
         i  = m(l)
         j  = m(nl+l)
         k  = m(2*nl+l)
         d1 = d(l)
         d2 = d(nl+l)
         d3 = d(2*nl+l)
         da = abs(d1)
         df(i,j,k) = h2*(d1*(-3.0d0*f(i,j,k)+4.0d0*f(i+int(d1),j,k)
     $                       -      f(i+2*int(d1),j,k)) +
     $               (1.0d0-da)*(f(i+1,j,k)-f(i-1,j,k) ) )
      end do
      return
      end

      subroutine diffx_ob(h,f,df)
      use params
      implicit none
      real*8, dimension(nx,ny,nz) :: f,df
      real*8  h,h2,hi
      integer i,j,k
!HPF$ PROCESSORS PROC(nproc)
!HPF$ DISTRIBUTE f *(BLOCK,*,*) ONTO *PROC
!HPF$ ALIGN(:,:,:) WITH *f(:,:,:)         :: df
      hi = 1.0d0/h
      h2 = 0.5d0 / h
      FORALL (k=1:nz,j=1:ny)
         df(1,j,k) = h2 * ( -3.0d0*f(1,j,k)
     .             + 4.0d0*f(1+1,j,k) - f(1+2,j,k) )
         df(nx,j,k) = h2 * (  3.0d0*f(nx,j,k)
     .              - 4.0d0*f(nx-1,j,k) + f(nx-2,j,k) )
      END FORALL
      FORALL (i=2:nx-1,k=1:nz)
            df(i,1,k) = h2 *(f(i+1,1,k)-f(i-1,1,k) )
            df(i,ny,k) = h2 *(f(i+1,ny,k)-f(i-1,ny,k) )
      END FORALL
      FORALL (i=2:nx-1,j=1:ny)
            df(i,j,1) = h2 *(f(i+1,j,1)-f(i-1,j,1) )
            df(i,j,nz) = h2 *(f(i+1,j,nz)-f(i-1,j,nz) )
      END FORALL

      return
      end