Stereographic Coordinate Patches method, is a new method for dealing with the computational problems which arise in the use of spherical coordinates. The method employs two stereographic coordinate patches, with interpolations in the region of overlap.
This method has been applied to the numerical solution of the 3-D wave equation.The program for this has been written in FORTRAN 77
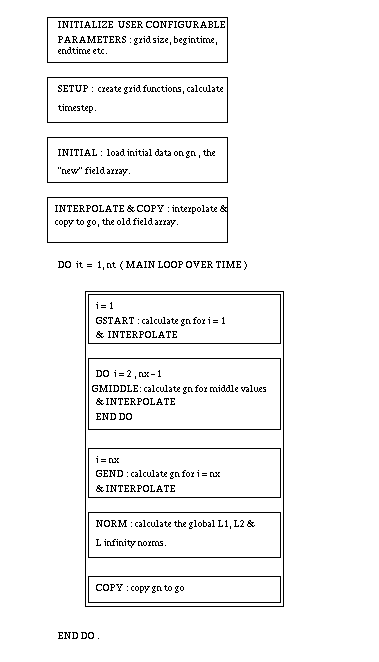
The structure of the Fortran 77 code is as follows:

Our objective is to try and parallelize this code. Right now, we are working at converting the code to FORTRAN 90 with the ultimate objective being conversion to HPF
As can be seen from the program structure, the major amount of computation time is spent in the routines GMIDDLE and INTERPOLATE.So our top priority is to parallelize these routines.
The subroutine GMIDDLE basically consists of three loops without any data dependences between successive iterations, and can be easily converted to Fortran 90 using FORALL statements. This conversion has already been implemented.
The subroutine INTERPOLATE presents a great challenge for parallelizing. An important observation to be made about this routine is that it operates only on the boundaries, whereas "appears" to operate over the entire field array. Althuogh there appears to be no parallelism immediately apparent, rewriting this routine using appropriate array sections, and not IF (or WHERE) should reveal parallelism. The routine operates only on that portion of the array, for which the value of the mask is non-zero. For a better understanding of the operation of the routine it would be instructional to look at the Structure of the array Mask.
The next set of routines that interest us are GSTART,GEND, NORM and COPY.
The routines GSTART and GEND are similar to the routine GMIDDLE and hence can be converted using the same principles.
Even though the routine NORM does not seem to be parallelizable at first glance,it is actually just calculating the value of "diff" for different values of k,l and i and is then computing the sum of all these values to form l1 and the sum of the squares of these values to form l2. The value of linfinity is determined from the last value of "diff".This kind of a structure can be easily implemented by using the fortran 90 FORALL statement and the SUM function for arrays.
The routine COPY just copies the values of the "new field array" to the "old field array", using three simple DO loops. This format can be easily handled by the FORALL statement.
The routines SETUP and INITIAL basically contain some loops which can be parallelized.