Scientific Applications

The highest profile applications in computational science are the so-called ``Grand Challenges''. [12] At the last count, there are 39 ``official'' grand challenge applications in the areas of chemistry, biology, biochemistry, physics, fluid dynamics, the environment, weather forecasting, geophysics, space science and astronomy, and artificial intelligence, which are deemed to be of national importance. Most grand challenge problems involve partial differential equations, particle dynamics, multidisciplinary integration, with some visualization and artificial intelligence. These are all amenable to parallel processing, and can all be expressed in HPF.

Most of the basic problems of this kind, for example solving differential equations, can be done using regular and often local algorithms. HPF can express these types of algorithms very well, and they will generally run very efficiently on MIMD, SIMD and vector architectures. However in many cases, the traditional algorithms have been superseded by modern, more effective algorithms, which are often non-local (e.g. multi-grid) and/or irregular (e.g. adaptive mesh). However the properties of non-locality and irregularity which help make these algorithms so effective, also make them difficult to implement efficiently on a vector or parallel supercomputer. In some cases it is also not obvious how to express this kind of algorithm in HPF.

This is an important issue for HPF: what applications does it support, and what extensions are needed to cover those applications not currently supported? [7, 14] A survey of approximately 400 scientific applications [11] gave the following classification of problems:

 
     		 Problem Class				 Number	        		 HPF Support

     		 Synchronous 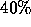				   				 Now

     		 Embarrassingly Parallel	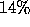		   				 Now

     		 Loosely Synchronous	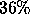		   				 Future

     		 Asynchronous	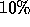			   				 No

HPF can currently handle synchronous problems, using data parallel arrays manipulated using intrinsic functions (shift, multiply, add, sum, etc.). Examples include:

• Regular grid partial differential equation solvers (e.g. finite difference)
• Regular ``crystalline'' particle interactions (e.g. lattice models of high energy physics theories such as quantum chromodynamics, spin models of magnets)
• Particle dynamics using O N-body algorithms
• Fast Fourier Transforms
• Dense matrix algorithms
• Low level image processing

The INDEPENDENT construct in HPF can be used for embarrassingly parallel problems, such as:

• Database searching (e.g. DOWQUEST [17])
• Monte Carlo calculations summed over independent simulations
• Analysis of independent data sets (e.g. real time analysis of millions of events from a particle collider using a MIMD farm)
• Calculation of matrix elements for computational chemistry (e.g. using MOPAC, GAUSSIAN)

Irregular loosely synchronous problems should be implementable in HPF, for example by using the FORALL statement, the PARTI routines for handling irregular communications and data distribution, [18] or library functions. These kinds of problems can usually only be implemented efficiently on MIMD machines, and in some cases even this is very difficult. Examples include:

• Particle dynamics with cutoff forces and irregular spatial structure
  (e.g. CHARMM, AMBER)
• Unstructured finite element meshes (static and adaptive)
• Connected component labeling (e.g. image processing, Monte Carlo simulation of spin models)

Problems which probably cannot be expressed in HPF in its current form include extremely irregular problems such as:

• Multiple phase problems (e.g. particle in cell, unstructured multigrid)
• Some O( ) or O(N) fast multipole methods for N-body particle dynamics
• Direct methods for sparse matrix solvers (general methods are very hard to parallelize and give modest performance)

Asynchronous problems such as transaction analysis and event driven simulation are outside the current (and anticipated future) scope of HPF.

Some irregular applications cannot currently be expressed in HPF, or at least not nearly as efficiently as in message passing languages. However the more common irregular applications such as sparse matrix solvers will be incorporated into HPF using software libraries, so the difficulties of the parallelism are hidden in a library call.

Some example applications are described in the following sub-sections. These algorithms are included in a suite of applications codes used to help validate and evaluate the Fortran 90D compiler. [31] This is being expanded into an HPFF application suite, which is being used as ``experimental data'' to test and evaluate the HPF language design, and may eventually evolve into a test suite to certify an HPF compiler.

• Component Labeling
• N-Body Particle Dynamics
• Random Surface Simulations