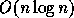 and we
can find the minimum length edge in
and we
can find the minimum length edge in 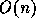 time.
time.
CIS600 HOMEWORK #3
Prepared by Hasan Timucin OZDEMIR
Wed Sep 18 09:02:56 EDT 1996
2. Calculate the delaunay diagram by using both of two sets. The edges of
delaunay diagram is the nearest neighbor of the point. Then we search the
edges whose endpoints are came from the different sets and the length is
minimum. Since we can find the delaunay diagram in 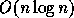 and we
can find the minimum length edge in
and we
can find the minimum length edge in 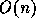 time.
time.
3. Let 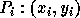 ,
, 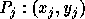 ,
,
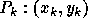 then
then
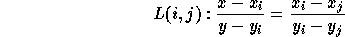
The vertical distance will be the distance between two points  and
and
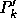 such that
such that  has the same
has the same 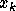 coordinate
value but
coordinate
value but 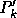 is on the L(i,j). Thus,
is on the L(i,j). Thus,

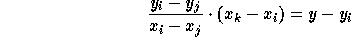
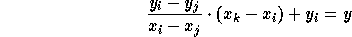
So the vertical distance 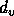
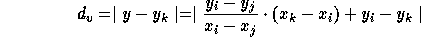
Let's look at the distance value in dual plane. We need to figure out L(i,j,k) on the primal plane,

Since L(i,j,k) is parallel to L(i,j)
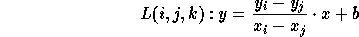
Let's find the value of b. Since  is on L(i,j,k),
is on L(i,j,k), 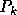 should
satisfy the line equation
should
satisfy the line equation

Then

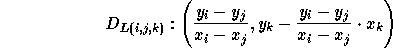
Since these two points are on the same x-coordinate value then the
vertical distance 
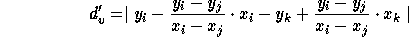
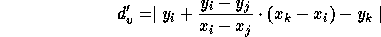
Since 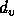 and
and  are equal, the claim is correct.
are equal, the claim is correct.
4. We know that if L intersects a polygon P, some of the points on the polygon is one side of line L and some of the points on the polygon is another side of the line L. If we map point (a,b) to line y=ax+b and line y=ax+b to point (-a,b). Then this mapping provides the following
Property : A point is to the left of a line if and only if the dual line is to the left of the dual point.
n-vertex of convex polygon P in the primal plane defines a convex polygon
in the dual plane. Since the point-line relationship in the primal plane
still holds in the dual plane as a line-point relationship. Thus, the problem
turns out to be a point location in the dual plane. We can do this test in
in  time, then the algorithm looks like the following
time, then the algorithm looks like the following
Preprocessing
 )
)
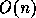 )
)
Query of given line L
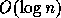 )
)