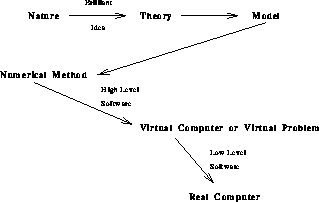
Figure 1: Computation and Simulation as a Series of Maps
We have described our classification of problem architectures several times before, but here we just summarize it.
This classification [Angus:90a], [Denning:90a], [Fox:88b;90p;91g;94a], was deduced from our experience at Caltech combined with a literature survey that was reasonably complete up to the middle of 1989. At Caltech, we developed some 50 applications on parallel machines, 25 of which led to publications in the scientific literature, describing the results of simulations performed on our parallel computers [Fox:87d] [Fox:88a], [Fox:88oo], [Fox:89n]. Our Caltech work was mainly on the hypercube, but the total of 300 references used in original classification covered work on the Butterfly, transputers, the SIMD Connection Machine, and DAP. We originally identified three temporal structures and one especially important (as it was so simple) spatial structure, which are the first four entries in Table 4. Chapter 3 of [Fox:94a] describes a ``complex systems'' approach to computation and introduces the spatial and temporal structure of problems and computers. We studied software as a mapping (Figure 1) of problems to computers with the software structure determined by the structure (architecture) of both the individual complex systems---computers and problems---and their interrelation. In Figure 2, we summarize issues in the spatial-temporal plane. ``Space'' here refers to data (problem) or nodes and their linkage (computer). ``Time'' is iteration number and simulation time (problem) or counts clock cycles (computer).

Figure 1: Computation and Simulation as a Series of Maps
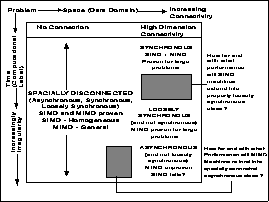
Figure 2: Issues Affecting Relation of Machine, Problem, and Software
Architecture
The three general temporal structures are called synchronous, loosely synchronous, and asynchronous. The temporal structure of a problem is analogous to the hardware classification into SIMD and MIMD. Further detail is contained in the spatial structure or computational graph of Figure 3a describing the problem at a given instant of simulation time [Fox:88tt]. This is important in determing the performance, as shown in Chapter 3 of [Fox:94a] of an implementation, but it does not affect the broad software issues discussed here. In Table 4, we only single out one special spatial structure, ``embarrassingly parallel,'' where there is little or no connection between the individual parallel program components. For embarrassingly parallel problems, illustrated in Figure 4, the synchronization (both software and hardware) issues are greatly simplified.
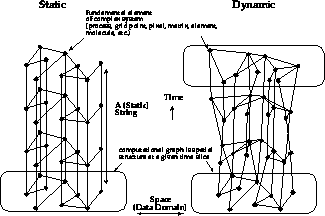
Figure 3: (a) Synchronous, Loosely Synchronous (Static), and (b)
Asynchronous (Dynamic) Complex Systems with their Space-Time Structure
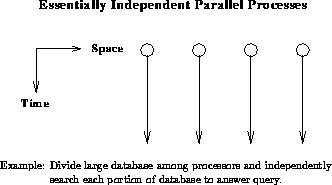
Figure 4: Embarrassingly Parallel Problem Class
Synchronous problems are data parallel in the language of Hillis [Hillis:87a] with the restriction that the time dependence of each data point is governed by the same algorithm. Both algorithmically and in the natural SIMD implementation, the problem is synchronized microscopically at each computer clock cycle. Such problems are particularly common in academic applications as they naturally arise in any description of some world in terms of identical fundamental units. This is illustrated in Figure 5 by quantum chromodynamics (QCD) simulations of the fundamental elementary particles that involve a set of gluon and quark fields on a regular four-dimensional lattice. These computations form one of the largest use of supercomputer time in academic computing.

Figure 5: The Synchronous Problem Class
Loosely synchronous problems are also typically data parallel, but now we allow different data points to be evolved with distinct algorithms. Such problems appear whever one describes the world macroscopically in terms of the interactions between irregular inhomogeneous objects evolved in a time synchronized fashion. Typical examples, as in Figure 6, are computer or biological circuit simulations where different components or neurons are linked irregularly and modelled differently. Time driven simulations and iterative procedures are not synchronized at each microscopic computer clock cycle, but rather only macroscopically ``every now and then'' at the end of an iteration or a simulation time step.
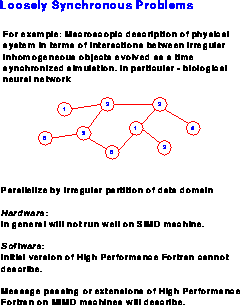
Figure 6: The Loosely Synchronous Problem Class
Loosely synchronous problems are spatially irregular, but temporally regular. The final asynchronous class is irregular in space and time, as in Figure 3b. A good example is an event driven simulation, illustrated in Figure 7, that can be used to describe the irregular circuits we discussed above, but now the event paradigm replaces the regular time stepped simulation. Other examples include computer chess [Felten:88i] and transaction analysis. Asynchronous problems are hard to parallelize and some may not run well on massively parallel machines. They require sophisticated software and hardware support to properly synchronize the nodes of the parallel machine, as is illustrated by time warp mechanism [Wieland:89a].
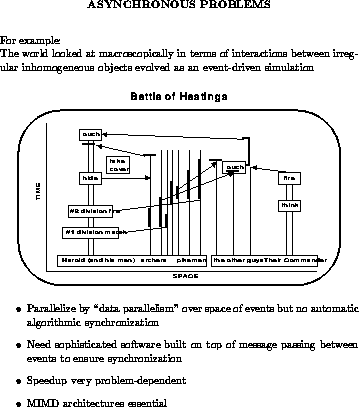
Figure 7: The Asynchronous Problem Class
Both synchronous and loosely synchronous problems parallelize on systems with many nodes. The algorithm naturally synchronizes the parallel components of the problem without any of the complex software or hardware synchronization mentioned above for event driven simulations. In the original survey, 90% of the surveyed applications fell into the classes that parallelize well. This includes 14% from the embarrassingly parallel classes, and roughly equal (38% each) amounts from synchronous or loosely synchronous class. It is interesting that massively parallel distributed memory MIMD machines that have an asynchronous hardware architecture are perhaps most relevant for loosely synchronous scientific problems.
We have looked at many more applications since the detailed survey in
[Fox:88b], and the general picture described above remains valid.
Industrial applications have less synchronous and more loosely
synchronous problems than academic problems. We have recently
recognized that many complicated problems are mixtures of the basic
classifications. The first major example with which I was involved was
a battle management simulation implemented by my collaborators at JPL
[Meier:89a]. This is formally asynchronous with temporally and
spatially irregular interconnections between various modules, such as
sensors for control platforms and input/output tasks. However, each
module uses a loosely synchronous algorithm, such as the multi-target
Kalman filter [Gottschalk:90b] or the target-weapon pairing
system. Thus, the whole metaproblem consists of a few (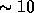 --50)
large grain asynchronous objects, each of which is a data parallel
synchronous or loosely synchronous algorithm. This type of
asynchronous problem can be implemented in a scaling fashion on
massively parallel machines. We call this a metaproblem or
asynchronous combination of several synchronous or loosely synchronous
problems. A similar example of this asynchronous or embarrassingly
synchronous problem class is machine vision and signal processing,
where one finds an asynchronous collection of data parallel modules to
perform various image processing tasks, such as stereo matching and
edge detection. Figure 8 illustrates another example
where we outline an approach to designing a new airframe that involves
aerodynamics, structures, radar signature, and the optimization
discussed later in Section 5.2. This figure also points out the
interesting analogy between heterogeneous metaproblems of class and a
heterogeneous computer network.
--50)
large grain asynchronous objects, each of which is a data parallel
synchronous or loosely synchronous algorithm. This type of
asynchronous problem can be implemented in a scaling fashion on
massively parallel machines. We call this a metaproblem or
asynchronous combination of several synchronous or loosely synchronous
problems. A similar example of this asynchronous or embarrassingly
synchronous problem class is machine vision and signal processing,
where one finds an asynchronous collection of data parallel modules to
perform various image processing tasks, such as stereo matching and
edge detection. Figure 8 illustrates another example
where we outline an approach to designing a new airframe that involves
aerodynamics, structures, radar signature, and the optimization
discussed later in Section 5.2. This figure also points out the
interesting analogy between heterogeneous metaproblems of class and a
heterogeneous computer network.
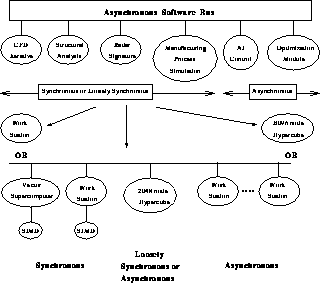
Figure 8: The Mapping of Heterogeneous Metaproblems onto Heterogeneous
Metacomputer Systems
In the above cases, the asynchronous components of the problems were large grain modules with modest parallelism. This can be contrasted with Otto and Felten's MIMD computer chess algorithm, where the asynchornous evaluation of the pruned tree is ``massively parallel'' [Felten:88i]. Here, one can break the problem up into many loosely coupled but asynchronous parallel components, which give excellent and scalable parallel performance. Each asynchronous task is now a synchronous or loosely synchronous modestly parallel evaluation of a given chess position.
There were a few examples mentioned above of metaproblems in our original survey, but a major part of Table 4, from our New York State activity, is the Information Integration classification, including manufacturing and the applications 25--33 are essentially all metaproblems. As stated boldly in Table 1, this class is the most important long-term area for HPCC. Further, as in battle management case, many problems that formerly appear asynchronous and were classified in this way in our original survey, are in fact metaproblems. Thus, the parallelism does not come from the difficult (impossible?) asynchronous structure, but the synchronous or loosely synchronous components buried inside the asynchronous shell. Thus, we believe metaproblems and their software support very important.