We have described our classification of problem architectures several times before, but here we just summarize it.
This classification [Angus:90a], [Denning:90a],
[Fox:88b;90p;91g;94a],
was deduced from our experience at
Caltech combined with a literature survey that was reasonably complete
up to the middle of 1989. At Caltech, we developed some 50
applications on parallel machines, 25 of which led to publications in
the scientific literature, describing the results of simulations
performed on our parallel computers [Fox:87d] [Fox:88a],
[Fox:88oo], [Fox:89n]. Our Caltech work was mainly on the
hypercube, but the total of 300 references used in original
classification covered work on the Butterfly, transputers, the SIMD
Connection Machine, and DAP. We originally identified three temporal
structures and one especially important (as it was so simple) spatial
structure, which are the first four entries in Table 3. Chapter 3 of
[Fox:94a] describes a ``complex systems'' approach to
computation and introduces the spatial and temporal structure of
problems and computers. We studied software as a mapping
(Figure 
) of problems to computers with the software
structure determined by the structure (architecture) of both the
individual complex systems---computers and problems---and their
interrelation. In Figure , we summarize issues in the
spatial-temporal plane. ``Space'' here refers to data (problem) or
nodes and their linkage (computer). ``Time'' is iteration number and
simulation time (problem) or counts clock cycles (computer).
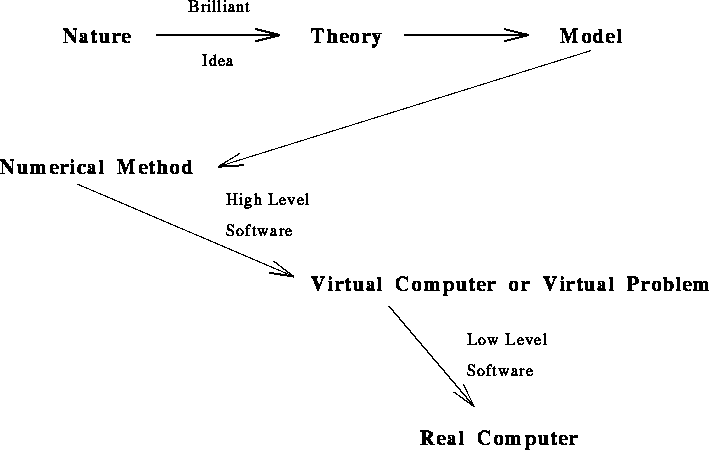
Figure: Computation and Simulation as a Series of Maps
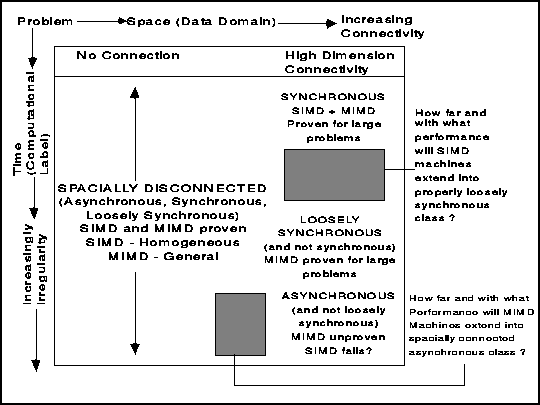
Figure: Issues Affecting Relation of Machine, Problem, and Software
Architecture
The three general temporal structures are called synchronous, loosely
synchronous, and asynchronous. The temporal structure of a problem is
analogous to the hardware classification into SIMD and MIMD. Further
detail is contained in the spatial structure or computational graph of
Figure a describing the problem at a given instant of
simulation time [Fox:88tt]. This is important in determining the
performance, as shown in Chapter 3 of [Fox:94a] of an
implementation, but it does not affect the broad software issues
discussed here. In Table 3, we only single out one special spatial
structure, ``embarrassingly parallel,'' where there is little or no
connection between the individual parallel program components. For
embarrassingly parallel problems, illustrated in
Figure , the synchronization (both software and
hardware) issues are greatly simplified.
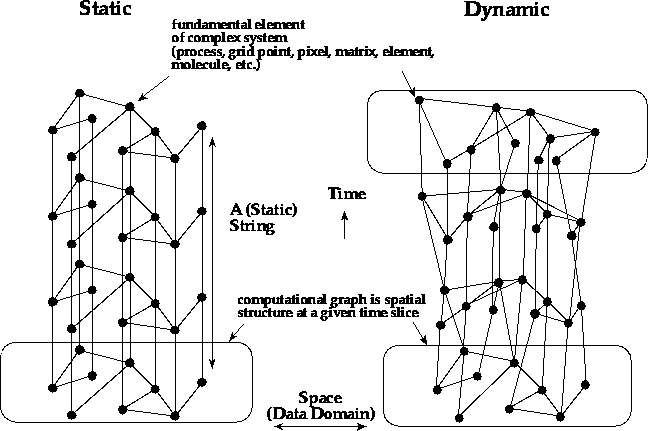
Figure: (a) Synchronous, Loosely Synchronous (Static), and (b)
Asynchronous (Dynamic) Complex Systems with their Space-Time Structure
Figure: Embarrassingly Parallel Problem Class
Synchronous problems are data parallel in the language of
Hillis [Hillis:87a] with the restriction that the time dependence
of each data point is governed by the same algorithm. Both
algorithmically and in the natural SIMD implementation, the problem is
synchronized microscopically at each computer clock cycle. Such
problems are particularly common in academic applications as they
naturally arise in any description of some world in terms of identical
fundamental units. This is illustrated in Figure by
quantum chromodynamics (QCD) simulations of the fundamental elementary
particles that involve a set of gluon and quark fields on a regular
four-dimensional lattice. These computations form one of the largest
use of supercomputer time in academic computing.
Figure: The Synchronous Problem Class
Loosely synchronous problems are also typically data parallel,
but now we allow different data points to be evolved with distinct
algorithms. Such problems appear whenever one describes the world
macroscopically in terms of the interactions between irregular
inhomogeneous objects evolved in a time synchronized fashion. Typical
examples, as in Figure , are computer or biological
circuit simulations where different components or neurons are linked
irregularly and modeled differently. Time driven simulations and
iterative procedures are not synchronized at each microscopic computer
clock cycle, but rather only macroscopically ``every now and then'' at
the end of an iteration or a simulation time step.
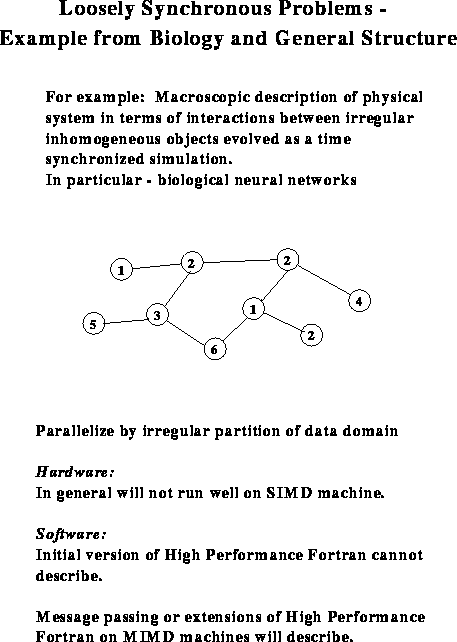
Figure: The Loosely Synchronous Problem Class
Loosely synchronous problems are spatially irregular, but temporally
regular. The final asynchronous class is irregular in space
and time, as in Figure b. A good example is an event
driven simulation, illustrated in Figure , that can be
used to describe the irregular circuits we discussed above, but now the
event paradigm replaces the regular time stepped simulation. Other
examples include computer chess [Felten:88i] and transaction
analysis. Asynchronous problems are hard to parallelize and some may
not run well on massively parallel machines. They require sophisticated
software and hardware support to properly synchronize the nodes of the
parallel machine, as is illustrated by time warp mechanism
[Wieland:89a].
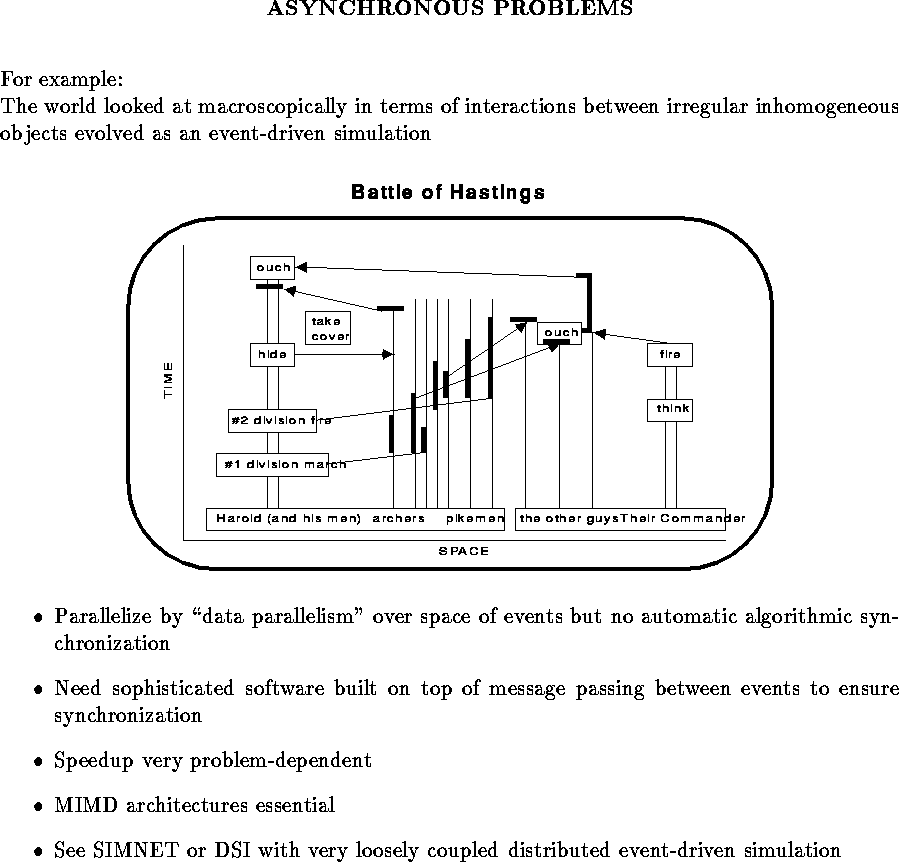
Figure: The Asynchronous Problem Class
Both synchronous and loosely synchronous problems parallelize on systems with many nodes. The algorithm naturally synchronizes the parallel components of the problem without any of the complex software or hardware synchronization mentioned above for event driven simulations. In the original survey, 90% of the surveyed applications fell into the classes that parallelize well. This includes 14% from the embarrassingly parallel classes, and roughly equal (38% each) amounts from synchronous or loosely synchronous class. It is interesting that massively parallel distributed memory MIMD machines that have an asynchronous hardware architecture are perhaps most relevant for loosely synchronous scientific problems.
We have looked at many more applications since the detailed survey in
[Fox:88b], and the general picture described above remains valid.
Industrial applications have less synchronous and more loosely
synchronous problems than academic problems. We have recently
recognized that many complicated problems are mixtures of the basic
classifications. The first major example with which I was involved was
a battle management simulation implemented by my collaborators at JPL
[Fox:94a], [Meier:89a]. This is formally asynchronous with
temporally and spatially irregular interconnections between various
modules, such as sensors for control platforms and input/output tasks.
However, each module uses a loosely synchronous algorithm, such as the
multi-target Kalman filter [Gottschalk:90b] or the target-weapon
pairing system. Thus, the whole metaproblem consists of a few (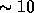
--50) large grain asynchronous objects, each of which is a data
parallel synchronous or loosely synchronous algorithm. This type of
asynchronous problem can be implemented in a scaling fashion on
massively parallel machines. We call this a metaproblem or
asynchronous combination of several synchronous or loosely synchronous
problems. A similar example of this asynchronous or embarrassingly
synchronous problem class is machine vision and signal processing,
where one finds an asynchronous collection of data parallel modules to
perform various image processing tasks, such as stereo matching and
edge detection. Figure illustrates another example
where we outline an approach to designing a new airframe that involves
aerodynamics, structures, radar signature, and the optimization
discussed later in Section . This figure also points out the
interesting analogy between heterogeneous metaproblems, and a
heterogeneous computer network. Section and
Figure gives a more concrete example of such a
metaproblem, which as usual, involves both database (I/O), and
computational subproblems.
Figure: The Mapping of Heterogeneous Metaproblems onto Heterogeneous
Metacomputer Systems
In the above cases, the asynchronous components of the problems were large grain modules with modest parallelism. This can be contrasted with Otto and Felten's MIMD computer chess algorithm, where the asynchronous evaluation of the pruned tree is ``massively parallel'' [Felten:88i]. Here, one can break the problem up into many loosely coupled but asynchronous parallel components, which give excellent and scalable parallel performance. Each asynchronous task is now a synchronous or loosely synchronous modestly parallel evaluation of a given chess position.
The World Wide Web is an enormous metasystem with many task parallel subproblems (Web servers handling many connections). Examples include data or task parallel ``applets'' handling computationally intense client computing for financial modeling, or a VRML rendering job. Data parallelism occurs in large data mining sub-applications on servers with links to Java or VRML clients, that just handle visualization and interpretation modules.
There were a few examples of metaproblems in our
original survey, but a major part of Table 4, from our New York State
activity, is the Information Integration classification. This class
includes manufacturing and the applications 25--33, all examples of
metaproblems. As stated boldly in Table 1, this class is the most
important long-term area for HPCC, and is discussed in
Sections and . Further, as in battle management
case, many problems that formerly appear asynchronous and were
classified in this way in our original survey, are in fact
metaproblems. Thus, the parallelism does not come from the difficult
(impossible?) asynchronous structure, but the synchronous or loosely
synchronous components buried inside the asynchronous shell. Thus, we
believe metaproblems and their software support to be very important.