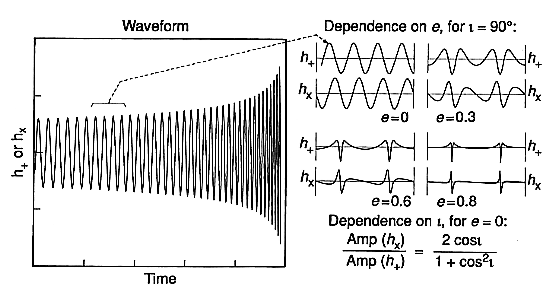
Figure 1 shows two components of a gravitational wave versus time
-
An example of gravitational waveforms and the information they carry.
-
Each gravitational wave has two waveforms, dimensionless functions of time called h+(t) and hx(t).
-
The specific waveforms shown here are from the last few minutes or seconds of the spiraling together of a compact binary system (one made of two black holes, two neutron stars, or a black hole and a neutron star).
-
By monitoring these waveforms, LIGO can allow researchers to determine the binary's distance from Earth r, the masses of its two bodies or, equivalently, their total mass M and reduced mass m, and their orbital eccentricity e, and orbital inclination to the line of sight i.
-
To allow the determination of the eccentricity e, LIGO will measure the shapes of the individual waveform oscillations; note the shape shown on the upper right.
-
For the determination of i (when e = 0 for pedagogic simplicity), LIGO will measure the ratio of the amplitudes, h+ and hx see the formula in the lower right.
-
The parameters r, m and M determine (i) the waveforms' absolute amplitudes as they sweep past a frequency f:
-
hamp proportional to mu M^2/3 r^-1 f^2/3;
-
and (ii) the number of cycles n=f^2 (df/dt)^-1 that the waveforms spend near frequency f:
-
n**alpha (mu M^2/3 f^5/3)^-1 .
-
From hamp and n, LIGO can be used to determine r and mu M^2/3.
-
From mu M^2/3, and from late-time post-Newtonian facets of the waveform (not shown here)
-
or the frequency at which the inspiral terminates or both,
-
LIGO can be used to deduce the individual value of mu and M.
-
The simple inspiral waves shown here are modified at late times by post-Newtonian
-
and then fully relativistic effects and then are followed by much more complicated waveforms from the final collision or tidal disruption of the black holes or neutron stars.
-
It is these final relativistic, collision, and disruption waveforms that will bring LIGO the most interesting information.
|
Basic IMAGE version of Foils prepared 15 March 1996
