Parallel computing is general purpose because there is a single
unifying mechanism on which it is based---this is called domain
decomposition or data parallelism. Nature solves complex problems by
dividing them up and assigning particular neurons, or group of
neurons, to different parts of the problem. This is illustrated in
Figure 4, which shows that different areas of the brain
are responsible for disentangling tactile information from different
parts of the body. Again, vision is a major task for the brain and
there is direct spatial mapping of received pixels of light at the
retina to neurons in the brain.
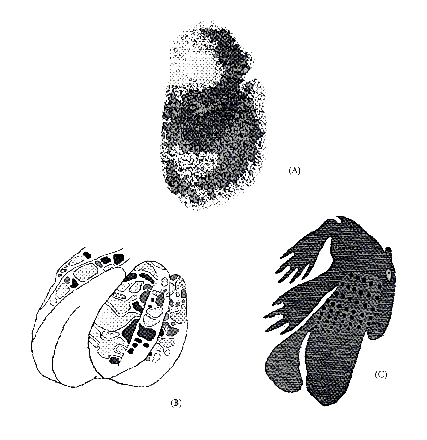
Figure 4: Three Parallel Computing Strategies Found in the Brain (of a
Rat). Each figure depicts brain activity corresponding to various
functions: (A) continuous map of a tactile inputs in somatosensory
cortex, (B) patchy map of tactile inputs to cerebellar cortex, and (C)
scattered mapping of olfactory cortex as represented by the
unstructured pattern of 2DG update in a single section of this cortex
[Nelson:90b].
Parallel simulation of interacting particles, shown in
Figure 5, is handled by data parallelism with individual
particles being assigned to a particular node in the parallel machine.
The astrophysical simulation of Figure 5 is very
inhomogeneous and corresponding the spatial regions assigned to a node
are irregular and indeed time dependent. This complexity was
challenging for the implementation, but the resultant program achieved
excellent performance with a speedup of over 800 on a 1024-node
nCUBE.
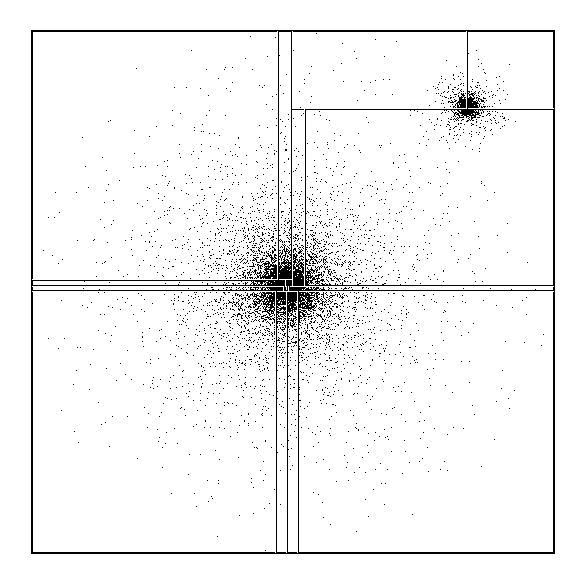
Figure 5: A Two-dimensional Projection of a Model Universe in which Two
Galaxies are on a Collision Course. This is a simplified version with
18,000 ``stars'' of a large simulation reported in [Salmon:89b]. The
irregular decomposition onto a 16-node machine is illustrated above.
Many large scale computations, such as those from the fields of
chemistry and electromagnetism, involve generation and manipulation of
large full matrices that represent the interaction Hamiltonian.
Energy level calculations involve eigenvalue determination while
scattering can use matrix multiplication and linear equation solution.
The same concept of data parallelism is used with, as seen in
Figure 6, a simple regular decomposition of the matrix
onto the processors. Parallelism is present both for generation of
the matrix elements that proceed independently in each node, and the
eigenvalue and other matrix operations. A general matrix library,
SCALAPACK is available for a broad class of high-performance
vector and parallel computers.

Figure 6: 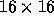 Matrix Decomposed onto a
Matrix Decomposed onto a 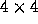 Parallel
Computer Array
Parallel
Computer Array
Problems consist of algorithms applied to a large data domain. Data
parallelism achieves parallelism by splitting up domain and applying
the computational algorithm concurrently to each point.



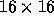 Matrix Decomposed onto a
Matrix Decomposed onto a 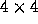 Parallel
Computer Array
Parallel
Computer Array