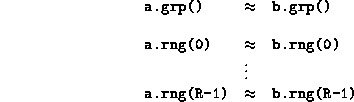
An array, a is aligned with an array b if they are distributed over the equivalent process groups and their ranges are all equivalent:
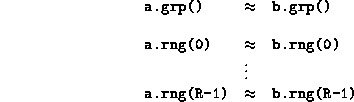
We omit full formal definition of alignment equivalence between groups
and ranges. Informally, two groups or two ranges are equivalent if
they are structurally equivalent
. The
informal meaning of array alignment is that corresponding elements of
the two arrays are stored on the same process, or replicated over the
same group of processes.
An array, a is value-aligned with an array b if their ranges are all equivalent and a.grp() contains b.grp(). The informal meaning of value-alignment is that every process that holds a copy of an element of b holds a copy of the corresponding element of a (although the converse may not be true, because a can be replicated over a larger process group).
Note that for value-alignment it is required that ranges are equivalent. A common mistake is to assume if a particular range of b is collapsed, but a has replicated alignment with respect to the corresponding range of b, the arrays satisfy the criteria for value-alignment. Informally this situtation seems to meet the requirements for value-alignment. Unfortunately it does not satisfy the strict definition, and in general functions that assume value-alignment will not work unless the strict definition is adhered to.
The array, a is aligned with b with replicated-alignment in some dimensions if the groups are equivalent, and the ranges of a can be paired with equivalent ranges of b by omitting the ranges of b associated with the specified dimensions. Value-alignment with replication in specified dimensions is defined similarly.