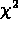Mean and Standard Deviation of

• Notice that is the sum 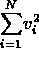where 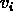are independent Gaussian random variables of unit standard deviation and zero mean.

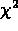• We can calculate the distribution exactly (Mathews and Walker pages 393--395) but in practice this is rarely necessary.

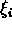• Thus, we can easily show that---for fixed ---that

  

  and this is sufficient for large N as central limit theorem says 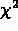will be Gaussian with above mean and standard deviation.

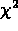• Now Equation (20) is not quite correct because if we determine the theoretical parameters to minimize , then implicitly 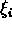are also random variables that are functions of .

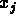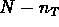• It is not too hard to show that in this case one should just replace N by (number of degrees of freedom) in (20).

• In any case, (20) is very important because it allows an easy criterion for the goodness of fit.