


Next: Means---Moments---Correlations for Multidimensional
Up: 1: Basic Definitions
Previous: Means---Momentsetc. for
 Given n-dimensional distribution
Given n-dimensional distribution 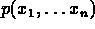 :
:
- The mean now becomes an n-dimensional vector
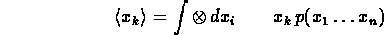
- The variance becomes an
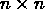 moment matrix
M
moment matrix
M
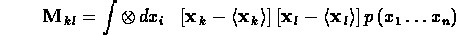
- Note for we can show---analogously to Equation (9)---that

- Also note that M is symmetric and positive semi-definite.
[This follows because
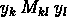 ---any y---clearly has a
---any y---clearly has a
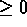 integrand].
integrand].
- Now the diagonal terms of M are called variances which are
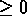 :
:
- Their square roots are standard deviations again.
- Further, when
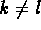 , we put
, we put
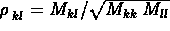 ,
which is
,
which is 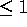 and is called the correlation coefficient.
and is called the correlation coefficient.
Geoffrey Fox, Northeast Parallel Architectures Center at Syracuse University, gcf@npac.syr.edu
 Given n-dimensional distribution
Given n-dimensional distribution 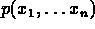 :
:
 Given n-dimensional distribution
Given n-dimensional distribution 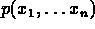 :
:
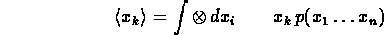
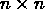 moment matrix
M
moment matrix
M
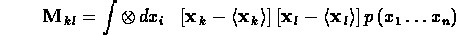

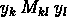 ---any y---clearly has a
---any y---clearly has a
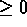 integrand].
integrand].
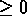 :
:
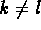 , we put
, we put
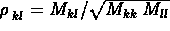 ,
which is
,
which is 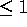 and is called the correlation coefficient.
and is called the correlation coefficient.