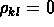 ---all
---all 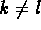 ---then we say that
---then we say that
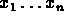 are uncorrelated.
are uncorrelated.
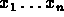 are independent, then Equation (10)
shows at once that they are uncorrelated.
are independent, then Equation (10)
shows at once that they are uncorrelated.
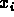 Gaussianly distributed).
Gaussianly distributed).
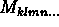 but these
are not too important as in usual applications
but these
are not too important as in usual applications 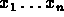 are n
functions of N>>n observations.
are n
functions of N>>n observations.
 Then central limit theorem---to which we will
come---implies that only the mean and
Then central limit theorem---to which we will
come---implies that only the mean and 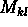 are important
asymptotically (in N).
are important
asymptotically (in N).