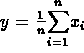 :
: 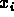 independent
independent
 (a) If
(a) If 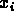 are Gaussian, then so is y: in fact,
if y Gaussian exactly, then so must all the
are Gaussian, then so is y: in fact,
if y Gaussian exactly, then so must all the 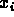 be Gaussian.
be Gaussian.
 (b) De Moivre in 1733 showed that if
(b) De Moivre in 1733 showed that if 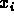 binomially
distributed, then y was always Gaussian for large x (even though
Gauss didn't exist in 1733).
binomially
distributed, then y was always Gaussian for large x (even though
Gauss didn't exist in 1733).
 (c) Laplace, in 1812, showed that de Moivre's result
was generally true for all distributions of
(c) Laplace, in 1812, showed that de Moivre's result
was generally true for all distributions of 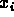 .
.
If 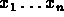 are independent random variables with the same
distribution, then y is asymptotically Gaussian with mean
are independent random variables with the same
distribution, then y is asymptotically Gaussian with mean 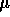 and
standard deviation
and
standard deviation 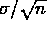 (where
(where 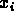 has mean
has mean 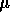 and standard
deviation
and standard
deviation 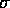 , and both
, and both 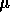 and
and 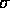 exist, i.e., are finite).
exist, i.e., are finite).