


Next: Proof of Central
Up: 1: Basic Definitions
Previous: Central Limit Theorem
- This extended theorem reads:
- If
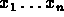 are independent random variables with
possibly different distributions, and:
are independent random variables with
possibly different distributions, and:

- where
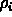 must exist (not necessary in Laplace's
version where all
must exist (not necessary in Laplace's
version where all 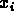 had same distribution).
had same distribution).
- Let

- Then if
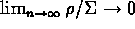 ,
,
- then y is Gaussianly distributed with
 mean
mean 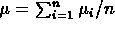 and
and
 standard deviation
standard deviation 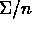 .
.
- Note the
 does
does
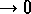 when
when 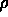 exists in Laplace's case as
exists in Laplace's case as 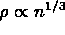 and
and 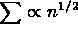 .
.
Geoffrey Fox, Northeast Parallel Architectures Center at Syracuse University, gcf@npac.syr.edu
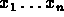 are independent random variables with
possibly different distributions, and:
are independent random variables with
possibly different distributions, and:

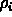 must exist (not necessary in Laplace's
version where all
must exist (not necessary in Laplace's
version where all 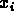 had same distribution).
had same distribution).

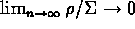 ,
,
 mean
mean 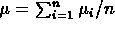 and
and
 standard deviation
standard deviation 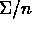 .
.
 does
does
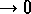 when
when 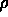 exists in Laplace's case as
exists in Laplace's case as 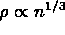 and
and 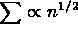 .
.