Evolution equation for the 3-metric

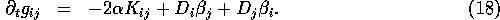
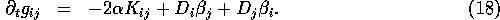
The evaluation of the second and third terms is carried out by once again using 9 temporary grid functions. Recall that 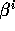, the contravariant form of the shift, is stored. Since 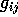is compatible with 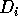we can rewrite 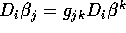. Hence we are left with calculating

Here once again we use a 9 grid functions to store the components of 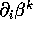first and then add 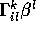to form eqn. (19). Then evaluating eqn. () becomes a matter of using the temporary variables for .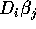

Use second order finite differencing for time derivative. 5 Modules for these routines

C in evolve_g1
      call diff(nx,ny,nz,h,beta1,t11,'x',ml,dl,nl)
      call diff(nx,ny,nz,h,beta1,t12,'y',ml,dl,nl)
      call diff(nx,ny,nz,h,beta1,t13,'z',ml,dl,nl)
      call diff(nx,ny,nz,h,beta2,t21,'x',ml,dl,nl)
      call diff(nx,ny,nz,h,beta2,t22,'y',ml,dl,nl)
      call diff(nx,ny,nz,h,beta2,t23,'z',ml,dl,nl)
      call diff(nx,ny,nz,h,beta3,t31,'x',ml,dl,nl)
      call diff(nx,ny,nz,h,beta3,t32,'y',ml,dl,nl)
      call diff(nx,ny,nz,h,beta3,t33,'z',ml,dl,nl)
C in evolve_g2
      FORALL (i=1:3,j=1:3)
         t(i,j) = t(i,j)+c(1,i,j)*beta(1)+c(2,i,j)*beta(2)
     .            +c(3,i,j)*beta(3)
      END FORALL
      FORALL (i=1:3,j=1:3)
         t(i,j) = t(i,1) * g(1,j) + t(i,2) * g(2,j) + t(i,3) * g(3,j)
      END FORALL
C in evolve_g3
      FORALL (j=1:3,i=1:3,i<=j)
         t(i,j) = t(i,j) + t(j,i) 
         t(j,i) = t(i,j)
      END FORALL
C in evolve_g4
      FORALL (i=1:3,j=1:3)
         t(i,j) = t(i,j) - 2.0d0*alpha(1) * ( g(1,i) * k(1,j) +
     .            g(2,i) * k(2,j) + g(3,i) * k(3,j)  )
      END FORALL
C in evolve_g5
      FORALL (j=1:3,i=1:3,i<=j)
         g(i,j,1) = 2.0d0*dt*t(i,j) + g(i,j,-1)
      END FORALL